题目内容
【题目】已知直线l:y=x+m,m∈R.
(I)若以点M(2,0)为圆心的圆与直线l相切与点P,且点P在y轴上,求该圆的方程;
(II)若直线l关于x轴对称的直线为![]() ,问直线
,问直线![]() 与抛物线C:x2=4y是否相切?说明理由.
与抛物线C:x2=4y是否相切?说明理由.
【答案】(I)![]()
(II)当m=1时,直线![]() 与抛物线C相切;当
与抛物线C相切;当![]() 时,直线
时,直线![]() 与抛物线C不相切.
与抛物线C不相切.
【解析】
(1)依题意,点P的坐标为(0,m)
因为圆与直线l相切与点P,∴MP⊥l![]()
![]() ,
,
解得m=2,即点P的坐标为(0,2)
从而圆的半径r=![]() =
=![]()
故所求圆的方程为![]() ;
;
(2)因为直线l的方程为y=x+m,
所以直线lˊ的方程为y=-x-m代入![]() 得
得![]()
∵![]() ∴m=1时
∴m=1时![]() ,即直线lˊ与抛物线C相切
,即直线lˊ与抛物线C相切
当m≠1时,![]() ,即直线lˊ与抛物线C不相切
,即直线lˊ与抛物线C不相切
综上,当m=1时,直线lˊ与抛物线C相切;
当m≠1时,直线lˊ与抛物线C不相切.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意,仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了![]() ,
,![]() 两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对
两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对![]() ,
,![]() 两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
|
| |
男业主 | 35 | 15 |
女业主 | 25 | 25 |
(1)分别估计![]() ,
,![]() 方案获得业主投票的概率;
方案获得业主投票的概率;
(2)判断能否有95%的把握认为投票选取管理方案与性别有关.
附: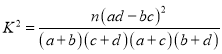 .
.
|
|
|
|
|
|
|
|