题目内容
已知点A(-1,0)、点B(2,0),动点C满足 ,则点C与点P(1,4)的中点M的轨迹方程为 .
,则点C与点P(1,4)的中点M的轨迹方程为 .
 ,则点C与点P(1,4)的中点M的轨迹方程为 .
,则点C与点P(1,4)的中点M的轨迹方程为 .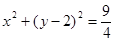
解:因为A(-1,0)、点B(2,0),动点C满足 =3,则点C的轨迹为圆心为(-1,0)半径为3的圆,那么点点C与点P(1,4)的中点M的坐标关系,利用中点公式得到,利用点随着点动,代入法得到轨迹方程为
=3,则点C的轨迹为圆心为(-1,0)半径为3的圆,那么点点C与点P(1,4)的中点M的坐标关系,利用中点公式得到,利用点随着点动,代入法得到轨迹方程为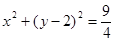
 =3,则点C的轨迹为圆心为(-1,0)半径为3的圆,那么点点C与点P(1,4)的中点M的坐标关系,利用中点公式得到,利用点随着点动,代入法得到轨迹方程为
=3,则点C的轨迹为圆心为(-1,0)半径为3的圆,那么点点C与点P(1,4)的中点M的坐标关系,利用中点公式得到,利用点随着点动,代入法得到轨迹方程为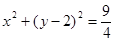

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
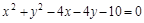 上的点到直线
上的点到直线 的最大距离是_________。
的最大距离是_________。 和曲线
和曲线 有两个不同的交点,则
有两个不同的交点,则 的取值范围是( )
的取值范围是( ) 



 与
与 轴相切于点
轴相切于点 ,与
,与 轴正半轴相交于两点
轴正半轴相交于两点 (点
(点 在点
在点 的左侧),且
的左侧),且 .
.
 相交于两点
相交于两点 ,连接
,连接 ,求证:
,求证: .
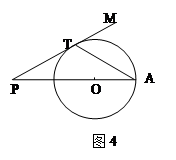
. 为圆
为圆 的切线,
的切线, 为切点,
为切点, ,圆
,圆 ,则
,则 .
.
 +
+ -4x-6y-12=0上至少有三点到直线4x-3y=m的距离是4,则m的取值范围是( )
-4x-6y-12=0上至少有三点到直线4x-3y=m的距离是4,则m的取值范围是( ) :3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.
:3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点. 表示的曲线为圆,则
表示的曲线为圆,则 的取值范围是( )
的取值范围是( ) .
. .
. 
