题目内容
已知椭圆的中心在原点,准线方程为x=±4,如果直线 :3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.
:3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.
(1)求椭圆方程;
(2)设直线 与椭圆的一个交点为P,F是椭圆的一个焦点,试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系;
与椭圆的一个交点为P,F是椭圆的一个焦点,试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系;
(3)把(2)的情况作一推广:写出命题(不要求证明)
 :3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.
:3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.(1)求椭圆方程;
(2)设直线
 与椭圆的一个交点为P,F是椭圆的一个焦点,试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系;
与椭圆的一个交点为P,F是椭圆的一个焦点,试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系;(3)把(2)的情况作一推广:写出命题(不要求证明)
解:(1)设椭圆方程为 (a>b>0)
(a>b>0)
直线3x-2y=0与椭圆的一个交点的坐标是 ,代入椭圆方程得:
,代入椭圆方程得:
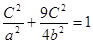 又
又 a2=b2+c2
a2=b2+c2
∴ a=2 C=1
C=1
∴ ………………5分
………………5分
(2)由(1)知,直线与椭圆的一个交点为 ,F(1,0),则从PF为直径的圆的方程
,F(1,0),则从PF为直径的圆的方程 ,圆心为
,圆心为 ,半径为
,半径为
以椭圆长轴为直径的圆的方程为x2+y2=4,圆心(0,0),半径为2
两圆圆心之间距离为
∴两圆内切 ………………8分
P、F为其它三种情况时,两圆都为内切 ………………10分
(3)如果椭圆的方程是 (a>b>0),P是椭圆上的任意一点,F是椭圆的一个焦点,则以PF长为直径的圆与以椭圆长轴为直径的圆是内切关系。 …………13分
(a>b>0),P是椭圆上的任意一点,F是椭圆的一个焦点,则以PF长为直径的圆与以椭圆长轴为直径的圆是内切关系。 …………13分
(如P写成椭圆上的定点,此问只给1分)
 (a>b>0)
(a>b>0)直线3x-2y=0与椭圆的一个交点的坐标是
 ,代入椭圆方程得:
,代入椭圆方程得: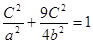 又
又 a2=b2+c2
a2=b2+c2∴ a=2
 C=1
C=1∴
 ………………5分
………………5分(2)由(1)知,直线与椭圆的一个交点为
 ,F(1,0),则从PF为直径的圆的方程
,F(1,0),则从PF为直径的圆的方程 ,圆心为
,圆心为 ,半径为
,半径为
以椭圆长轴为直径的圆的方程为x2+y2=4,圆心(0,0),半径为2
两圆圆心之间距离为

∴两圆内切 ………………8分
P、F为其它三种情况时,两圆都为内切 ………………10分
(3)如果椭圆的方程是
 (a>b>0),P是椭圆上的任意一点,F是椭圆的一个焦点,则以PF长为直径的圆与以椭圆长轴为直径的圆是内切关系。 …………13分
(a>b>0),P是椭圆上的任意一点,F是椭圆的一个焦点,则以PF长为直径的圆与以椭圆长轴为直径的圆是内切关系。 …………13分(如P写成椭圆上的定点,此问只给1分)
略

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 ,则点C与点P(1,4)的中点M的轨迹方程为 .
,则点C与点P(1,4)的中点M的轨迹方程为 . (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为 、
、 (其中
(其中 ).
).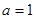 ,求
,求 与
与 的值;
的值; 与直线
与直线 相切,求圆
相切,求圆 ,且以点
,且以点 过圆
过圆 的圆心,则a的值为
的圆心,则a的值为 1
1 相切的圆的方程。
相切的圆的方程。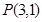 及两条直线
及两条直线 ,则过点
,则过点 且与两直线都相切的圆的方程是____________________________________________。
且与两直线都相切的圆的方程是____________________________________________。 的弧的中点为
的弧的中点为 ,动点
,动点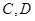 分别在线段
分别在线段 上,且
上,且 若
若 ,
, ,则
,则 的取值范围是
的取值范围是 
 +y
+y


 轴相切的圆的方程是
轴相切的圆的方程是


