Question

【题目】从正方体ABCD﹣A1B1C1D1的8个顶点中任意取4个不同的顶点，这4个顶点可能是：
1）矩形的4个顶点；
2）每个面都是等边三角形的四面体的4个顶点；
3）每个面都是直角三角形的四面体的4个顶点；
4）有三个面是等腰直角三角形，有一个面是等边三角形的四面体的4个顶点．
其中正确结论的个数为 ．

Answer 1

【答案】4
【解析】解：如图所示：
四边形ABCD为矩形，故（1）满足条件；
四面体D﹣A1BC1为每个面均为等边三角形的四面体，故（2）满足条件；
四面体D﹣B1C1D1为每个面都是直角三角形的四面体，故（3）满足条件；
四面体C﹣B1C1D1为有三个面是等腰直角三角形，有一个面是等边三角形的四面体，故（4）满足条件；
故正确的结论有4个
所以答案是：4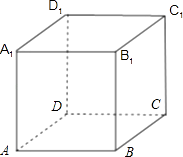

【考点精析】利用棱柱的结构特征对题目进行判断即可得到答案，需要熟知两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形．