题目内容
21.已知函数f（x）＝a·bx的图象过点A（4，
）和B（5，1）.（1）求函数f（x）的解析式；
（2）记an＝log2f（n），n是正整数，Sn是数列｛an｝的前n项和，解关于n的不等式anSn≤0；
（3）对于（2）中的an与Sn，整数104是否为数列｛anSn｝中的项？若是，则求出相应的项数；若不是，则说明理由.
21.
［解］（1）由＝a·b4，1＝a·b5，得b＝4，a＝
，故f（x）＝
4x.
（2）由题意an＝log2（
·4n）＝2n－10，
Sn＝
（a1＋an）＝n（n－9），
anSn＝2n（n－5）（n－9）.
由anSn≤0，得（n－5）（n－9）≤0，即5≤n≤9.
故n＝5，6，7，8，9.
（3）a1S1＝64，a2S2＝84，a3S3＝72，a4S4＝40.
当5≤n≤9时，anSn≤0.
当10≤n≤22时，anSn≤a22S22＝9724＜104.
当n≥23时，anSn≥a23S23＝11592＞104.
因此，104不是数列{anSn}中的项.
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
的图像过点A（4，
）和B（5，1）．
（n），n是正整数，
是数列{
}的前n项和，解关于n的不等式
；
与
，整数
是否为数列{
}中的项?若是，则求出相应的项数；若不是，则说明理由．
－x （e为自然对数的底数）．
≤x≤2}且M∩P≠
，求实数a的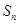
＝
（t为常数，t≥0），是否存在等比数列{
}，使得b1＋b2＋…
与x＝1时都取得极值。
）和B（5，1）.