题目内容
 (2012•泰州二模)已知函数f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x(a>0).
(2012•泰州二模)已知函数f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x(a>0).(1)若函数f(x)在x=0处取极值,求a的值;
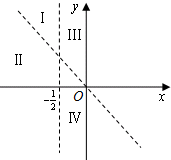
(2)如图,设直线x=-
| 1 | 2 |
(3)比较32×43×54×…×20122011与23×34×45×…×20112012的大小,并说明理由.
分析:(1)由f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x得f′(x)=2ln(2x+1)-4a(2x+1)+1,由f(x)在x=0处取极值,能求出a.
(2)由函数的定义域为(-
,+∞),且当x=0时,f(0)=-a<0,又直线y=-x恰好过原点,所以函数y=f(x)的图象应位于区域Ⅲ内,于是f(x)<-x,由此能求出a的取值范围.
(3)由(2)知,函数m(x)=
在x∈(
,+∞)时单调递减,函数p(x)=
在x∈(e,+∞)时,单调递减,故 (x+1)x<x(x+1),由此能比较32×43×54×…×20122011与23×34×45×…×20112012的大小.
(2)由函数的定义域为(-
| 1 |
| 2 |
(3)由(2)知,函数m(x)=
| ln(2x+1) |
| 2x+1 |
| e-1 |
| 2 |
| lnx |
| x |
解答:解:(1)∵f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x,
∴f′(x)=2ln(2x+1)-4a(2x+1)+1,
∵f(x)在x=0处取极值,
∴f′(0)=-4a+1=0,
∴a=
,经检验a=
符合题意,
故a=
.
(2)∵函数的定义域为(-
,+∞),且当x=0时,f(0)=-a<0,
又直线y=-x恰好过原点,
所以函数y=f(x)的图象应位于区域Ⅲ内,
于是f(x)<-x,
即 (2x+1)ln(2x+1)-a(2x+1)2-x<-x,
∵2x+1>0,∴a>
,
令h(x)=
,∴h′(x)=
,
令h′(x)=0,得x=
,
∵x>-
,∴x∈(-
,
)时,h′(x)>0,h(x)单调递增,
x∈(
,+∞)时,h′(x)<0,h(x)单调递减.
∴mmax(x)=m(
)=
,
∴a的取值范围是:a>
.
(3)由(2)知,函数m(x)=
在x∈(
,+∞)时单调递减,
∴函数p(x)=
在x∈(e,+∞)时,单调递减,
∴
<
,∴xln(x+1)<(x+1)lnx,
∴ln(x+1)x<lnx(x+1),即(x+1)x<x(x+1),
∴令x=3,4,…,2011,则43<34,54<45,…,20122011<20112012.
又32×43<23×34,
∴32×43×54×…×20122011<23×34×45×…×20112012.
∴f′(x)=2ln(2x+1)-4a(2x+1)+1,
∵f(x)在x=0处取极值,
∴f′(0)=-4a+1=0,
∴a=
| 1 |
| 4 |
| 1 |
| 4 |
故a=
| 1 |
| 4 |
(2)∵函数的定义域为(-
| 1 |
| 2 |
又直线y=-x恰好过原点,
所以函数y=f(x)的图象应位于区域Ⅲ内,
于是f(x)<-x,
即 (2x+1)ln(2x+1)-a(2x+1)2-x<-x,
∵2x+1>0,∴a>
| ln(2x+1) |
| 2x+1 |
令h(x)=
| ln(2x+1) |
| 2x+1 |
| 2-ln(2x+1) |
| (2x+1)2 |
令h′(x)=0,得x=
| e-1 |
| 2 |
∵x>-
| 1 |
| 2 |
| 1 |
| 2 |
| e-1 |
| 2 |
x∈(
| e-1 |
| 2 |
∴mmax(x)=m(
| e-1 |
| 2 |
| 1 |
| e |
∴a的取值范围是:a>
| 1 |
| e |
(3)由(2)知,函数m(x)=
| ln(2x+1) |
| 2x+1 |
| e-1 |
| 2 |
∴函数p(x)=
| lnx |
| x |
∴
| ln(x+1) |
| x+1 |
| lnx |
| x |
∴ln(x+1)x<lnx(x+1),即(x+1)x<x(x+1),
∴令x=3,4,…,2011,则43<34,54<45,…,20122011<20112012.
又32×43<23×34,
∴32×43×54×…×20122011<23×34×45×…×20112012.
点评:本题考查利用导数求闭区间上函数最值的应用,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意挖掘题中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
 (2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.