题目内容
(2012•泰州二模)若抛物线y2=2px(p>0)上的点A(2,m)到焦点的距离为6,则p=
8
8
.分析:利用抛物线的定义,将点A(2,m)到焦点的距离为6,转化为点A(2,m)到其准线的距离即可.
解答:解:∵抛物线y2=2px(p>0)的准线方程为:x=-
,焦点F(
,0),
又物线y2=2px(p>0)上的点A(2,m)到焦点的距离为6,
∴由抛物线的定义得:点A(2,m)到焦点的距离等于它到准线的距离,
∴2-(-
)=6,
∴p=8.
故答案为:8.
| p |
| 2 |
| p |
| 2 |
又物线y2=2px(p>0)上的点A(2,m)到焦点的距离为6,
∴由抛物线的定义得:点A(2,m)到焦点的距离等于它到准线的距离,
∴2-(-
| p |
| 2 |
∴p=8.
故答案为:8.
点评:本题考查抛物线的简单性质,着重考查抛物线的定义的应用,突出转化思想的考查,属于基础题.

练习册系列答案
相关题目
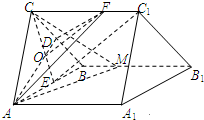 (2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.