题目内容
【题目】定义在[﹣1,1]上的函数f(x)满足:①对任意a,b∈[﹣1,1],且a+b≠0,都有 ![]() >0成立;②f(x)在[﹣1,1]上是奇函数,且f(1)=1.
>0成立;②f(x)在[﹣1,1]上是奇函数,且f(1)=1.
(1)求证:f(x)在[﹣1,1]上是单调递增函数;
(2)解关于x不等式f(x)<f( ![]() x+1);
x+1);
(3)若f(x)≤m2﹣2am﹣2对所有的x∈[﹣1,1]及a∈[﹣1,1]恒成立,求实数m的取值范围.
【答案】
(1)解:任取x1、x2∈[﹣1,1],且x1<x2,
则f(x1)﹣f(x2)=f(x1)+f(﹣x2)
∵ ![]() >0,x1﹣x2<0,
>0,x1﹣x2<0,
∴f(x1)﹣f(x2)<0.
则f(x)是[﹣1,1]上的增函数.
(2)解:若f(x)<f( ![]() x+1),则﹣1≤x<
x+1),则﹣1≤x< ![]() x+1≤1,
x+1≤1,
解得:x∈[﹣1,0],
故不等式f(x)<f( ![]() x+1)的解集为[﹣1,0];
x+1)的解集为[﹣1,0];
(3)解:要使f(x)≤m2﹣2am﹣2对所有的x∈[﹣1,1],a∈[﹣1,1]恒成立,
只须f(x)max≤m2﹣2am﹣2,即1≤m2﹣2am﹣2对任意的a∈[﹣1,1]恒成立,
亦即m2﹣2am﹣3≥0对任意的a∈[﹣1,1]恒成立.
令g(a)=m2﹣2am﹣3,
只须 ![]() ,
,
解得m≤﹣3或m≥3.
【解析】(1)利用函数单调性的定义进行证明:在区间[﹣1,1]任取x1、x2 , 且x1<x2 , 利用函数为奇函数的性质结合已知条件中的分式,可以证得f(x1)﹣f(x2)<0,所以函数f(x)是[﹣1,1]上的增函数.(2)根据(1)中单调性,可得﹣1≤x< ![]() x+1≤1,解得答案;(3)根据函数f(x)≤m2﹣2am﹣2对所有的x∈[﹣1,1],a∈[﹣1,1]恒成立,说明f(x)的最大值1小于或等于右边,因此先将右边看作a的函数,m为参数系数,解不等式组,即可得出m的取值范围.
x+1≤1,解得答案;(3)根据函数f(x)≤m2﹣2am﹣2对所有的x∈[﹣1,1],a∈[﹣1,1]恒成立,说明f(x)的最大值1小于或等于右边,因此先将右边看作a的函数,m为参数系数,解不等式组,即可得出m的取值范围.
【考点精析】通过灵活运用函数单调性的性质,掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集即可以解答此题.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】某市的教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的同学中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图(分组区间为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ),并将分数从低到高分为四个等级:
),并将分数从低到高分为四个等级:
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有340人.
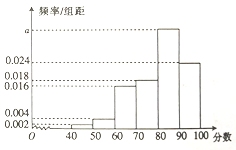
(1)求表中![]() 的值及不满意的人数;
的值及不满意的人数;
(2)在等级为不满意的师生中,老师占![]() ,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记
,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记![]() 为老师整改督导员的人数,求
为老师整改督导员的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元. (Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,n∈N)的函数解析式f(n);
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望.


