题目内容
函数y=f(x)(x∈R)满足:对一切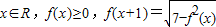 ,当
,当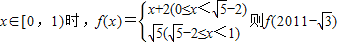 =( )
=( )A.
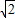
B.
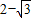
C.
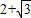
D.
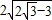
【答案】分析:先根据条件对一切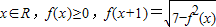 ,等式两边同时平方得f2(x+1)+f2(x)=7,根据递推关系可知f2(x+2)+f2(x+1)=7,两式相减可求出函数的周期,然后根据周期将f(2011-
,等式两边同时平方得f2(x+1)+f2(x)=7,根据递推关系可知f2(x+2)+f2(x+1)=7,两式相减可求出函数的周期,然后根据周期将f(2011-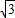 )化成f(3-
)化成f(3-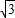 ),而f(2-
),而f(2-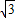 +1)=
+1)=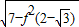 ,代入相应的解析式,解之即可求出所求.
,代入相应的解析式,解之即可求出所求.
解答:解:∵对一切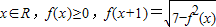 ,
,
∴f2(x+1)+f2(x)=7则f2(x+2)+f2(x+1)=7
两式相减得:f2(x+2)=f2(x)即f(x+2)=f(x)
∴f(2011-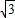 )=f(3-
)=f(3-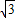 )=f(2-
)=f(2- +1)=
+1)=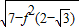
而2-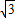 >
>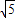 -2
-2
∴f(2-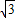 )=
)=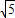
∴f(2011-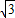 )=f(3-
)=f(3-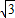 )=f(2-
)=f(2-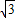 +1)=
+1)=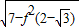 =
=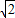
故选A
点评:本题主要考查了函数的值,以及函数的周期性,同时考查转化的思想,属于中档题.
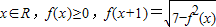 ,等式两边同时平方得f2(x+1)+f2(x)=7,根据递推关系可知f2(x+2)+f2(x+1)=7,两式相减可求出函数的周期,然后根据周期将f(2011-
,等式两边同时平方得f2(x+1)+f2(x)=7,根据递推关系可知f2(x+2)+f2(x+1)=7,两式相减可求出函数的周期,然后根据周期将f(2011-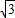 )化成f(3-
)化成f(3-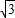 ),而f(2-
),而f(2-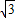 +1)=
+1)=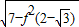 ,代入相应的解析式,解之即可求出所求.
,代入相应的解析式,解之即可求出所求.解答:解:∵对一切
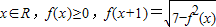 ,
,∴f2(x+1)+f2(x)=7则f2(x+2)+f2(x+1)=7
两式相减得:f2(x+2)=f2(x)即f(x+2)=f(x)
∴f(2011-
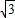 )=f(3-
)=f(3-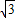 )=f(2-
)=f(2- +1)=
+1)=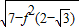
而2-
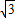 >
>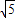 -2
-2∴f(2-
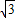 )=
)=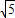
∴f(2011-
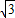 )=f(3-
)=f(3-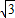 )=f(2-
)=f(2-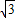 +1)=
+1)=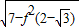 =
=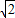
故选A
点评:本题主要考查了函数的值,以及函数的周期性,同时考查转化的思想,属于中档题.

练习册系列答案
相关题目