题目内容
(选作题)定义在(-1,1)上的函数y=f(x)满足:对任意x,y∈(-1,1)都有f(x)+f(y)=f(
).
(1)判断函数f(x)的奇偶性,并证明;
(2)如果当x∈(-1,0)时,有f(x)>0,求证:f(x)在(-1,1)上是单调递减函数;
(3)在(2)的条件下解不等式:f(x+
)+f(
)>0.
| x+y |
| 1+xy |
(1)判断函数f(x)的奇偶性,并证明;
(2)如果当x∈(-1,0)时,有f(x)>0,求证:f(x)在(-1,1)上是单调递减函数;
(3)在(2)的条件下解不等式:f(x+
| 1 |
| 2 |
| 1 |
| 1-x |
分析:(1)令x=y=0 可求得f(0)=0;令y=-x代入f(x)+f(y)=f(
)可判断f(x)的奇偶;
(2)设-1<x1<x2<1,利用f(x1)-f(x2)=f(x1)+f(-x2)=f(
),分析判断出-1<
<0,再结合条件即可证明结论;
(3)利用(1)f(x)为奇函数与(2)f(x)在(-1,1)上是单调递减函数将f(x+
)+f(
)>0转化为f(x+
) >f(
),脱掉f,化为不等式组解之即可.
| x+y |
| 1+xy |
(2)设-1<x1<x2<1,利用f(x1)-f(x2)=f(x1)+f(-x2)=f(
| x1-x2 |
| 1-x1•x2 |
| x1-x2 |
| 1-x1•x2 |
(3)利用(1)f(x)为奇函数与(2)f(x)在(-1,1)上是单调递减函数将f(x+
| 1 |
| 2 |
| 1 |
| 1-x |
| 1 |
| 2 |
| 1 |
| x-1 |
解答:解:(1)f(x)为奇函数.
令x=y=0,代入f(x)+f(y)=f(
)有,
2f(0)=f(0),f(0)=0;
令y=-x,代入f(x)+f(y)=f(
)得:
f(x)+f(-x)=f(0)=0,(xy≠-1,由定义域易知其满足)
∴f(x)=-f(-x),得证.
(2)设-1<x1<x2<1,
f(x1)-f(x2)=f(x1)+f(-x2)=f(
),
由题设知,必有-1<
<1
又x1-x2<0,由x1,x2∈(-1,1),可得-x1•x2∈(-1,1),所以1-x1•x2>0,
所以-1<
<0,又x∈(-1,0)时f(x)>0,
∴f(x1)-f(x2)=f(
)>0
∴f(x1)>f(x2)
即f(x)在(-1,1)上是减函数;
(3)∵f(x+
)+f(
)>0,f(x)为奇函数,
∴f(x+
) >f(
),函数y=f(x)定义在(-1,1)上,f(x)在(-1,1)上是单调递减函数,
∴
解得:-
<x<-1
∴不等式的解集为:{x|-
<x<-1}.
令x=y=0,代入f(x)+f(y)=f(
| x+y |
| 1+xy |
2f(0)=f(0),f(0)=0;
令y=-x,代入f(x)+f(y)=f(
| x+y |
| 1+xy |
f(x)+f(-x)=f(0)=0,(xy≠-1,由定义域易知其满足)
∴f(x)=-f(-x),得证.
(2)设-1<x1<x2<1,
f(x1)-f(x2)=f(x1)+f(-x2)=f(
| x1-x2 |
| 1-x1•x2 |
由题设知,必有-1<
| x1-x2 |
| 1-x1•x2 |
又x1-x2<0,由x1,x2∈(-1,1),可得-x1•x2∈(-1,1),所以1-x1•x2>0,
所以-1<
| x1-x2 |
| 1-x1•x2 |
∴f(x1)-f(x2)=f(
| x1-x2 |
| 1-x1•x2 |
∴f(x1)>f(x2)
即f(x)在(-1,1)上是减函数;
(3)∵f(x+
| 1 |
| 2 |
| 1 |
| 1-x |
∴f(x+
| 1 |
| 2 |
| 1 |
| x-1 |
∴
|
| 3 |
| 2 |
∴不等式的解集为:{x|-
| 3 |
| 2 |
点评:本题考查函数的性质,难点在于第(2)问函数单调性的证明中-1<
<0的分析,级第(3)解不等式组,综合考查学生的分析,计算及正确推理的能力,是难题.
| x1-x2 |
| 1-x1•x2 |

练习册系列答案
相关题目
 ,
,
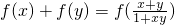 .
. .
.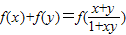 .
. .
.