Question

【题目】已知数列，，其前项和满足，其中.

（1）设，证明：数列是等差数列；

（2）设，为数列的前项和，求证：；

（3）设（为非零整数，），试确定的值，使得对任意，都有成立.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）.

【解析】试题分析：（1）当时，得到，当时，，即可化简，即可证得结论；（2）由（1）可得 ，利用乘公比错误相减法，即可求解数列的和；（3）由得，整理得，当为奇数时，，∴；当为偶数时，，∴，由为非零整数，即可求解．

试题解析：（1）当时，，∴，

当时，，

∴，即，∴（常数），

又，∴是首项为2，公差为1的等差数列，∴．

（2） ，

∴，

，

相减得 ，

∴．

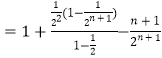
（3）由，得，

，

，，

当为奇数时，，∴；

当为偶数时，，∴，

∴，又为非零整数，∴．