题目内容
已知集合A={x|x2+3x-18>0}，B={x|(x-k)(x-k-1)≤0}，A∩B≠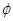
，则k的取值范围为( )
(A){k|k<-6或k>1} (B) {k|k<-2或k>3} (C) {k|k<-6或k>2} (D){k|k<-3或k>2}
【答案】
C
【解析】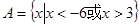
，又B={x|(x-k)(x-k-1)≤0}及A∩B≠
，则
，
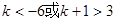所以k<-6或k>2，故选C
练习册系列答案
阅读快车系列答案
相关题目