题目内容
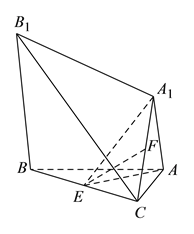
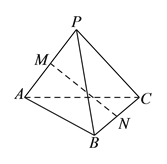
【题目】如图,三棱锥![]() 的三个侧面均为边长是
的三个侧面均为边长是![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
(I)求![]() 的长.
的长.
(II)求证: ![]() .
.
(III)求三棱锥![]() 的表面积.
的表面积.
【答案】(1) ![]() ;(2)详见解析;(3)
;(2)详见解析;(3) ![]() .
.
【解析】试题分析:(1) 连接![]() ,
, ![]() ,等边
,等边![]() 中,
中, ![]() ,
, 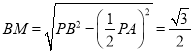 ,同理可得
,同理可得![]() ,等腰
,等腰![]() 中,
中, ![]() ,
, 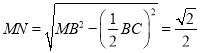 ;(2)由线面垂直的判定定理证明
;(2)由线面垂直的判定定理证明![]() 平面
平面![]() ,则
,则![]() ;(3) 三棱锥
;(3) 三棱锥![]() 的三个侧面均为边长为
的三个侧面均为边长为![]() 的等边三角形,底面
的等边三角形,底面![]() 仍为边长为
仍为边长为![]() 的等边三角形,分别求出各面的面积求和即三棱锥的表面积.
的等边三角形,分别求出各面的面积求和即三棱锥的表面积.
试题解析:
(I)连接![]() ,
, ![]() ,
,
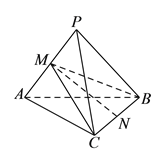
∵在等边![]() 中,
中,
![]() 是
是![]() 边上中点,
边上中点,
∴![]() ,
,
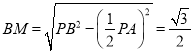 ,
,
同理可得![]() ,
,
在等腰![]() 中,
中,
![]() 为
为![]() 边上中点,
边上中点,
∴![]() ,
,
∴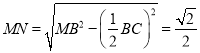 .
.
(II)证明:∵![]() ,
, ![]() ,
,
![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
(III)∵三棱锥![]() 的三个侧面均为边长为
的三个侧面均为边长为![]() 的等边三角形,
的等边三角形,
则底面![]() 中,
中, ![]() ,
,
∴底面![]() 仍为边长为
仍为边长为![]() 的等边三角形,
的等边三角形,
∴表面积![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.