题目内容

15．已知函数f（x）=excosx，则函数f（x）在点（0，f（0））处的切线方程为（　　）
A．y=1B．x-y+1=0C．x+y+1=0D．x-y=0

分析 求出f（x）的导数，切点切线的斜率和切点，由斜截式方程，即可得到切线的方程．

解答 解：函数f（x）=excosx的导数为f′（x）=ex（cosx-sinx），
函数f（x）在点（0，f（0））处的切线斜率为k=e0（cos0-sin0）=1，
切点为（0，1），
则函数f（x）在点（0，f（0））处的切线方程为y=x+1．
故选：B．

点评 本题考查导数的运用：求切线的方程，考查导数的几何意义，正确求导是解题的关键．

练习册系列答案
相关题目
5．已知函数f（x）=ax2+bx+c（a＞0且bc≠0）．
（Ⅰ）若|f（0）|=|f（1）|=|f（-1）|=1，试求f（x）的解析式；
（Ⅱ）令g（x）=2ax+b，若g（1）=0，又f（x）的图象在x轴上截得的弦的长度为l，且0＜l≤2，试比较b、c的大小．
6．已知一次函数f（x）是R上的增函数，g（x）=f（x）（x+m），且f（f（x））=16x+5
（1）求f（x）的解析式；
（2）若g（x）在（1，+∞）上单调递增，求实数m的取值范围．
3．如图圆柱的底面周长为4π，高为2，圆锥的底面半径是1，则该几何体的体积为$\frac{22π}{3}$
10．已知函数$f（x）=\left\{\begin{array}{l}\frac{1}{2}x，x≤0\\{x^2}-4x，x＞0\end{array}\right.$，若关于x的方程f（x）=m恰有三个互不相等的实数根x1，x2，x3，则x1x2x3的取值范围是（　　）
A．（-32，0）B．（-16，0）C．（-8，0）D．（-4，0）
20．函数$f（x）={x^3}-\sqrt{x}$的零点个数为2．
7．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一个焦点与抛物线y2=4x的焦点重合，则双曲线的离心率等于$\sqrt{5}$，则该双曲线的方程为$\frac{{x}^{2}}{\frac{1}{5}}-\frac{{y}^{2}}{\frac{4}{5}}$=1．
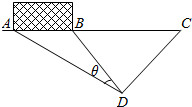4．如图所示，足球门左右门柱分别立在A、B处，假定足球门宽度AB为7米，在距离右门柱15米的C处，一球员带球沿与球门线AC成28°角的CD方向以平均每秒6.5米的速度推进，2秒后到达D处射门．问：
（1）D点到左右门柱的距离分别为多少米？
（2）此时射门张角θ为多少？（注：cos28°≈$\frac{23}{26}$）
5．如图．四棱锥P-ABCD，ABCD为矩形，E，F分别为AB，PC的中点，证明：EF∥平面PAD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网