Question

【题目】[选修4-5：不等式选讲]
已知函数f（x）=|x+1|﹣|2x﹣3|．

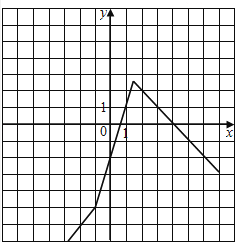
（1）在图中画出y=f（x）的图象；
（2）求不等式|f（x）|＞1的解集．

Answer 1

【答案】
（1）

解：f（x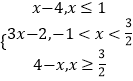）= ， 由分段函数的图象画法，可得f（x）的图象，如右：

（2）

解：由|f（x）|＞1，可得

当x≤﹣1时，|x﹣4|＞1，解得x＞5或x＜3，即有x≤﹣1；

当﹣1＜x＜ 时，|3x﹣2|＞1，解得x＞1或x＜ ，

即有﹣1＜x＜ 或1＜x＜ ；

当x≥ 时，|4﹣x|＞1，解得x＞5或x＜3，即有x＞5或 ≤x＜3．

综上可得，x＜ 或1＜x＜3或x＞5．

则|f（x）|＞1的解集为（﹣∞， ）∪（1，3）∪（5，+∞）

【解析】（Ⅰ）运用分段函数的形式写出f（x）的解析式，由分段函数的画法，即可得到所求图象；（2）分别讨论当x≤﹣1时，当﹣1＜x＜ 时，当x≥ 时，解绝对值不等式，取交集，最后求并集即可得到所求解集．；本题考查绝对值函数的图象和不等式的解法，注意运用分段函数的图象的画法和分类讨论思想方法，考查运算能力，属于基础题．