题目内容
【题目】在正方体ABCD﹣A1B1C1D1中,异面直线AD1与BD所成的角为;若AB的中点为M,DD1的中点为N,则异面直线B1M与CN所成的角为 .
【答案】60°;90°
【解析】解:由题意:ABCD﹣A1B1C1D1是正方体,BC1∥AD1 , 异面直线AD1与BD所成的角为∠DBC1 , 连接C1D,
可得:DB,C1D,BC1是正方形的对角线,
∴DB=C1D=BC1
所以△DBC1是等边三角形,
异面直线AD1与BD所成的角为∠DBC1=60°.
AB的中点为M,DD1的中点为N,
过M点作CN平形线交AA1于F,连接MF,
异面直线B1M与CN所成的角为∠FMB1 ,
设正方体的边长为a,则CN=MB1= ![]() ,
,
MF= ![]() CN=
CN= ![]() ,B1F=
,B1F= ![]() .
.
∵ ![]() .
.
∴FM⊥MB1
即异面直线B1M与CN所成的角为90°.
所以答案是:60°,90°.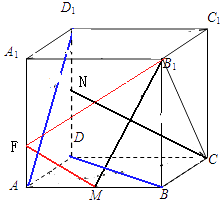
【考点精析】利用异面直线及其所成的角对题目进行判断即可得到答案,需要熟知异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
