题目内容
(10分)设函数![]() ,其中向量
,其中向量![]() =(sinx,-cosx),
=(sinx,-cosx),![]()
![]() =(sinx,-3cosx),
=(sinx,-3cosx),![]() =(-cosx,sinx),x∈R.
=(-cosx,sinx),x∈R.
(1) 求函数![]() 的单调减区间。
的单调减区间。
(2)函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样变化得出?
的图象经过怎样变化得出?
(3)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围。
的取值范围。
解:(1)由题意得
![]() =(sinx,-cosx)·(sinx-cosx,sinx-3cosx)
=(sinx,-cosx)·(sinx-cosx,sinx-3cosx)
=sin2x-2sinxcosx+3cos2x=2+cos2x-sin2x=![]() sin(2x+
sin(2x+![]() )…2分
)…2分

故![]() 的单调减区间为
的单调减区间为![]() ………4分
………4分
(2)先将![]() 的图象上所有点向右平移
的图象上所有点向右平移![]() 个单位,
个单位,
再将所得的图象上所有点横坐标压缩到原来的![]() ,
,
然后再将所得的图象上所有点纵坐标伸长到原来的![]() 倍,
倍,
最后将所得图象上所有点向上平移![]() 个单位即可得
个单位即可得![]() 的图象
的图象
………6分
(3) ∵![]() 在
在![]() 上恒成立
上恒成立
∴![]()
∴![]() 且
且 ![]()
即 ![]() 且
且 ![]()
∴![]() ………10分
………10分

练习册系列答案
相关题目

 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。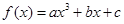
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。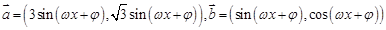 ,其中
,其中 ,设
,设 ,其周期为
,其周期为 ,且
,且 是它的一条对称轴。
是它的一条对称轴。 的解析式;
的解析式; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数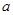 的取值范围。
的取值范围。 (
( ,
, ,
, )的图象的最高点D的坐标为
)的图象的最高点D的坐标为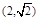 ,由最高点运动到相邻的最低点F时,曲线与
,由最高点运动到相邻的最低点F时,曲线与 轴相交于点
轴相交于点 .
. ,使其图象与
,使其图象与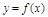 图象关于直线
图象关于直线 对称.
对称.