题目内容
(本题满分10分)
设函数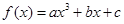
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。
【答案】
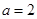 ,
,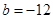 ,
,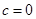 .
.
【解析】本试题主要是考查了导数在研究函数中的运用。
根据已知条件,函数的导数的几何意义,利用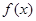 为奇函数,∴
为奇函数,∴
即 ∴
∴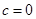 ∵
∵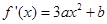 的最小值为
的最小值为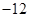 ∴
∴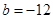 ,然后利用斜率知道参数a的值,得到结论。
,然后利用斜率知道参数a的值,得到结论。
解:∵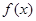 为奇函数,∴
为奇函数,∴
即 ∴
∴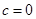 (4分)
(4分)
∵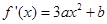 的最小值为
的最小值为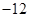 ∴
∴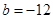 (6分)
(6分)
又直线 的斜率为
的斜率为 因此,
因此, (8分)
(8分)
∴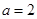 ,
,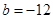 ,
,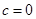 .(10分)
.(10分)

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,求证:
,求证: ;
; ,求证:三数
,求证:三数 ,
, ,
, 中至少有一个不小于2.
中至少有一个不小于2.
 的所有棱长都为2,
的所有棱长都为2, 为棱
为棱 的中点,
的中点, 平面
平面 ;
; 的余弦值大小.
的余弦值大小.
 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点