题目内容
【题目】已知函数f(x)=bax(a>0,且a≠1,b∈R)的图象经过点A(1,6),B(3,24).
(1)设g(x)= ![]() ﹣
﹣ ![]() ,确定函数g(x)的奇偶性;
,确定函数g(x)的奇偶性;
(2)若对任意x∈(﹣∞,1],不等式( ![]() )x≥2m+1恒成立,求实数m的取值范围.
)x≥2m+1恒成立,求实数m的取值范围.
【答案】
(1)解:∵f(x)=bax(a>0,且a≠1,b∈R)的图象经过点A(1,6),B(3,24),
∴ ![]() ,解得:a=2,b=3,
,解得:a=2,b=3,
∴f(x)=32x,
又g(x)= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴g(x)+g(﹣x)= ![]() +
+ ![]() ﹣
﹣ ![]() ×2=
×2= ![]() +
+ 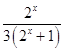 ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =0,
=0,
∴g(﹣x)=﹣g(x),
∴函数g(x)为奇函数
(2)解:由(1)知,a=2,b=3,
∴对任意x∈(﹣∞,1],不等式( ![]() )x≥2m+1恒成立2m+1≤[
)x≥2m+1恒成立2m+1≤[ ![]() ]min,x∈(﹣∞,1],
]min,x∈(﹣∞,1],
∵y= ![]() 为减函数,
为减函数,
∴当x∈(﹣∞,1]时,[ ![]() ]min=
]min= ![]() =
= ![]() ,
,
∴2m+1≤ ![]() ,
,
∴m≤﹣ ![]() ,
,
即实数m的取值范围为(﹣∞,﹣ ![]() ]
]
【解析】(1)依题意,可得 ![]() ,解得:a=2,b=3,即f(x)=32x , 故g(x)=
,解得:a=2,b=3,即f(x)=32x , 故g(x)= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,利用g(x)+g(﹣x)=0可确定函数g(x)的奇偶性;(2)任意x∈(﹣∞,1],不等式(
,利用g(x)+g(﹣x)=0可确定函数g(x)的奇偶性;(2)任意x∈(﹣∞,1],不等式( ![]() )x≥2m+1恒成立2m+1≤[
)x≥2m+1恒成立2m+1≤[ ![]() ]min , x∈(﹣∞,1],利用指数函数的单调性可求得当x∈(﹣∞,1]时,[
]min , x∈(﹣∞,1],利用指数函数的单调性可求得当x∈(﹣∞,1]时,[ ![]() ]min=
]min= ![]() =
= ![]() ,从而可求实数m的取值范围.
,从而可求实数m的取值范围.

练习册系列答案
相关题目