题目内容
已知函数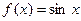 ,
,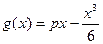
(I) 在(I)的条件下,求证:当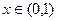 时,
时,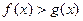 恒成立
恒成立
(II) 若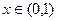 时
时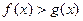 恒成立,求
恒成立,求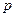 的取值范围
的取值范围
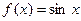 ,
,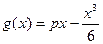
(I) 在(I)的条件下,求证:当
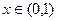 时,
时,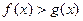 恒成立
恒成立(II) 若
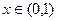 时
时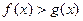 恒成立,求
恒成立,求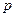 的取值范围
的取值范围(II) 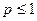
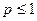
(I)设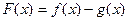
当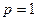 时,
时,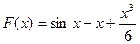 ,
,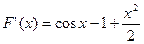 ,
,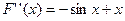
当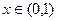 时,
时,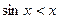 ,故
,故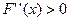 ,从而
,从而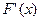 在
在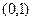 上单调递增,所以
上单调递增,所以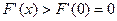 进而
进而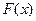 在
在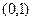 上单调递增,所以
上单调递增,所以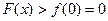 ,即
,即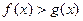 恒成立 ……8分
恒成立 ……8分
(II)当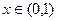 时,因为
时,因为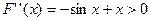 ,所以
,所以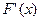 在
在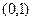 上单调递增,从而
上单调递增,从而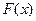 在
在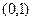 内不可能出现先增后减的情况
内不可能出现先增后减的情况
又因为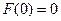 ,所以要使
,所以要使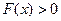 在
在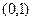 上恒成立,必有
上恒成立,必有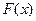 在
在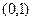 上单调递增,即
上单调递增,即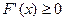 在
在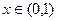 上恒成立,因为
上恒成立,因为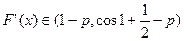 ,所以有
,所以有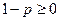 即
即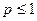 即为所求.
即为所求.
当
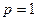 时,
时,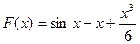 ,
,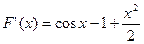 ,
,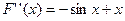
当
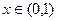 时,
时,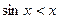 ,故
,故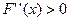 ,从而
,从而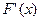 在
在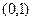 上单调递增,所以
上单调递增,所以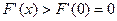 进而
进而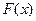 在
在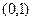 上单调递增,所以
上单调递增,所以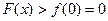 ,即
,即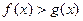 恒成立 ……8分
恒成立 ……8分(II)当
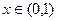 时,因为
时,因为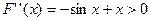 ,所以
,所以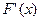 在
在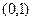 上单调递增,从而
上单调递增,从而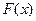 在
在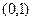 内不可能出现先增后减的情况
内不可能出现先增后减的情况又因为
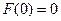 ,所以要使
,所以要使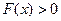 在
在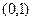 上恒成立,必有
上恒成立,必有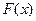 在
在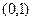 上单调递增,即
上单调递增,即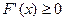 在
在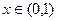 上恒成立,因为
上恒成立,因为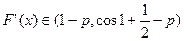 ,所以有
,所以有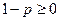 即
即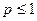 即为所求.
即为所求. 
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
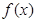 的定义域为
的定义域为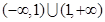 ,且
,且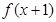 为奇函数,当
为奇函数,当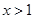 时,
时,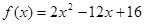 ,则直线
,则直线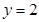 与函数
与函数
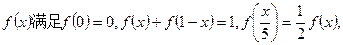 且当
且当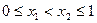 时,
时,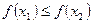 .则
.则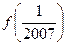 等于 ( )
等于 ( ) 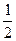
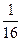
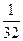
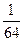
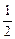 ,
,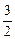 ],求函数g(x)=f(3x)+f(
],求函数g(x)=f(3x)+f(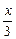 )的定义域
)的定义域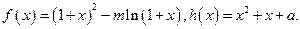
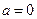 时,
时,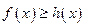 在
在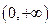 上恒成立,求实数的取值范围;
上恒成立,求实数的取值范围;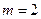 时,若函数
时,若函数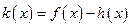 在
在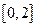 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数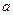 的取值范围;
的取值范围;


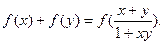
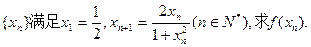
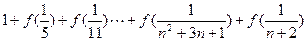 的值.
的值.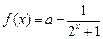
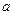 为何实数
为何实数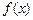 总是为增函数;(2)确定
总是为增函数;(2)确定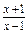 +log2(x-1)+log2(p-x).
+log2(x-1)+log2(p-x).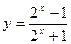 的值域是
的值域是