题目内容
（本题满分14分）
对于函数
，若存在
成立，则称
的不动点.如果函数
有且只有两个不动点0，2，且
（1）求函数的解析式；
（2）已知各项不为零的数列
，求数列通项
；
（3）如果数列
满足
，求证：当
时，恒有
成立.
（本小题满分14分）
解：设
得：
由违达定理得：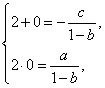
解得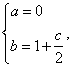
代入表达式
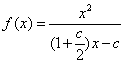，由
得
不止有两个不动点，
………………………………………5分
（2）由题设得
（A）
且
（B）
由（A）
（B）得：
解得
（舍去）或
；由，若
这与
矛盾，
，即{
是以1为首项，1为公差的等差数列，
； ………………………………………………………………10分
（3）证法（一）：运用反证法，假设
则由（1）知
∴
，而当
这与假设矛盾，故假设不成立，∴.………………………………………14分
证法（二）：由
得
<0或
结论成立；
若
，此时
从而
即数列{}在时单调递减，由
，可知
上成立.………………………………………………………………………………………14分
练习册系列答案
相关题目
为
上的点，且BF⊥平面ACE．
B=[0,3]，求实数m的值
CRB，求实数m的取值范围
是⊙
：
上的任意一点，过
垂直
轴于
,动点
满足
。
，在动点
、
，使
(O是坐标原点)，若存在，求出直线
的方程，若不存在，请说明理由。
.
的定义域；
是否有根?如果有根
，请求出一个长度为
的区间
，使
).