��Ŀ����
����������14��A��ѡ��4-4������������������ڼ�����ϵ�У�ֱ��l �ļ����귽��Ϊ��=
| �� |
| 3 |
|
B��ѡ��4-5������ʽѡ��
��ʵ��x��y��z ����x+y+2z=6����x2+y2+z2 ����Сֵ�������ʱx��y��z ��ֵ��
������A�� �ȵó�ֱ��l ����ͨ����Ϊy=
x��������C ��ֱ�����귽��Ϊy=
x2(x��[-2��2])�������ⷽ�����
��
�������P ���ֱ�����ꣻ
B������һ����ʽ�Ŀ�������ʽ�ó�����x2+y2+z2����12+12+22���ݣ�x+y+2z��2=36���Ӷ��ó���x2+y2+z2 ����Сֵ��
| 3 |
| 1 |
| 2 |
|
|
B������һ����ʽ�Ŀ�������ʽ�ó�����x2+y2+z2����12+12+22���ݣ�x+y+2z��2=36���Ӷ��ó���x2+y2+z2 ����Сֵ��
����⣺ֱ��l ����ͨ����Ϊy=
x��
����C ��ֱ�����귽��Ϊy=
x2(x��[-2��2])������4�֣�
�����ⷽ�����
��
����ȥ��
��P ���ֱ������Ϊ��0��0��������7�֣�
B���⣺�ߣ�x2+y2+z2����12+12+22���ݣ�x+y+2z��2=36��
�ࣨx2+y2+z2����6�����ҽ���x=y=
ʱȡ�Ⱥţ�����4�֣�
��x+y+2z=6����x=1��y=1��z=2��
��x2+y2+z2 ����СֵΪ6����ʱx=1��y=1��z=2������7�֣�
| 3 |
����C ��ֱ�����귽��Ϊy=
| 1 |
| 2 |
�����ⷽ�����
|
|
��P ���ֱ������Ϊ��0��0��������7�֣�
B���⣺�ߣ�x2+y2+z2����12+12+22���ݣ�x+y+2z��2=36��
�ࣨx2+y2+z2����6�����ҽ���x=y=
| z |
| 2 |
��x+y+2z=6����x=1��y=1��z=2��
��x2+y2+z2 ����СֵΪ6����ʱx=1��y=1��z=2������7�֣�
��������С����Ҫ��������ߵļ����귽�̡������ߵIJ������̡�һ����ʽ�Ŀ�������ʽ�Ȼ���֪ʶ�������������������ת��˼�룮���ڻ����⣮

��ϰ��ϵ�д�
�����Ŀ
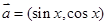 ��
��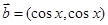 ��
��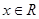 ������
������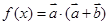
 �����ֵ����С�����ڣ�
�����ֵ����С�����ڣ� ������
������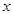 ��ȡֵ����.
��ȡֵ����.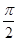 ����λ���ٰ�ͼ�����е�ĺ��������̵�ԭ����
����λ���ٰ�ͼ�����е�ĺ��������̵�ԭ����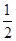 ���õ�
���õ�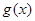 ������
������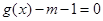 ��
�� ���ҽ���һ���⣬��
���ҽ���һ���⣬�� ��ȡֵ��Χ��
��ȡֵ��Χ��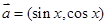 ��
��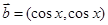 ��
��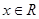 ������
������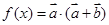
 �����ֵ����С�����ڣ�
�����ֵ����С�����ڣ�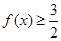 ������
������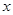 ��ȡֵ����.
��ȡֵ����.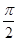 ����λ���ٰ�ͼ�����е�ĺ��������̵�ԭ����
����λ���ٰ�ͼ�����е�ĺ��������̵�ԭ����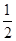 ���õ�
���õ�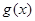 ������
������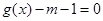 ��
��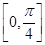 ���ҽ���һ���⣬��
���ҽ���һ���⣬�� ��ȡֵ��Χ��
��ȡֵ��Χ�� �Ľ⼯A��
�Ľ⼯A�� �IJ���ʽ
�IJ���ʽ �Ľ⼯Ϊ
�Ľ⼯Ϊ ����
���� ����ʵ��
����ʵ�� ��ȡֵ��Χ��
��ȡֵ��Χ��