题目内容
已知抛物线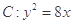 的焦点为
的焦点为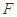 ,准线与
,准线与 轴的交点为
轴的交点为 ,点
,点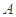 在
在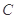 上且
上且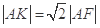 ,则
,则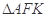 的面积为( )
的面积为( )
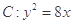 的焦点为
的焦点为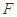 ,准线与
,准线与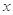 轴的交点为
轴的交点为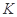 ,点
,点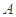 在
在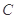 上且
上且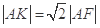 ,则
,则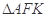 的面积为( )
的面积为( )A.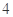 | B.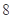 | C. | D.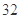 |
B
考点:
分析:根据抛物线的方程可知焦点坐标和准线方程,进而可求得K的坐标,设A(x0,y0),过A点向准线作垂线AB,则B(-2,y0),根据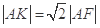 及AF=AB=x
及AF=AB=x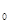 -(-2)= x
-(-2)= x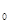 +2,进而可求得A点坐标,进而求得△AFK的面积.
+2,进而可求得A点坐标,进而求得△AFK的面积.
解答:解:∵抛物线C:y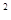 =8x的焦点为F(2,0),准线为x=-2
=8x的焦点为F(2,0),准线为x=-2
∴K(-2,0)
设A(x0,y0),过A点向准线作垂线AB,则B(-2,y0)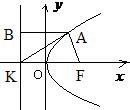
∵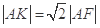 ,又AF=AB=x
,又AF=AB=x -(-2)= x
-(-2)= x +2,
+2,
∴由BK =AK
=AK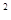 -AB
-AB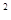 得y
得y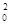 =(x
=(x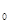 +2)
+2)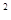 ,即8x
,即8x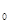 =(x
=(x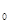 +2)
+2)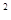 ,解得A(2,±4)
,解得A(2,±4)
∴△AFK的面积为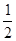 |KF|?|y
|KF|?|y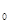 |=
|=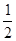 ×4×4=8
×4×4=8
故选B.
点评:此题重点考查双曲线的第二定义,双曲线中与焦点,准线有关三角形问题;由题意准确画出图象,利用离心率转化位置,在△ABK中集中条件求出x 是关键;
是关键;
分析:根据抛物线的方程可知焦点坐标和准线方程,进而可求得K的坐标,设A(x0,y0),过A点向准线作垂线AB,则B(-2,y0),根据
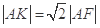 及AF=AB=x
及AF=AB=x -(-2)= x
-(-2)= x +2,进而可求得A点坐标,进而求得△AFK的面积.
+2,进而可求得A点坐标,进而求得△AFK的面积.解答:解:∵抛物线C:y
 =8x的焦点为F(2,0),准线为x=-2
=8x的焦点为F(2,0),准线为x=-2 ∴K(-2,0)
设A(x0,y0),过A点向准线作垂线AB,则B(-2,y0)

∵
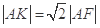 ,又AF=AB=x
,又AF=AB=x -(-2)= x
-(-2)= x +2,
+2,∴由BK
 =AK
=AK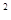 -AB
-AB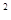 得y
得y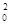 =(x
=(x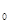 +2)
+2)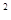 ,即8x
,即8x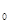 =(x
=(x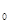 +2)
+2)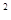 ,解得A(2,±4)
,解得A(2,±4)∴△AFK的面积为
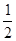 |KF|?|y
|KF|?|y |=
|=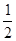 ×4×4=8
×4×4=8故选B.
点评:此题重点考查双曲线的第二定义,双曲线中与焦点,准线有关三角形问题;由题意准确画出图象,利用离心率转化位置,在△ABK中集中条件求出x
 是关键;
是关键;
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与抛物线
与抛物线 的准线相切,则
的准线相切,则 的值等于( )
的值等于( )
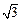
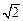
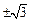
 ,直线
,直线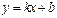 与椭圆
与椭圆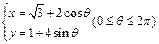 恒有公共点,则
恒有公共点,则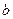 的
的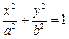
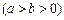 ,焦点为
,焦点为 、
、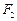 ,双曲线G:
,双曲线G:
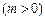 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线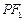 、
、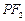 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形 的周长等于
的周长等于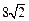 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为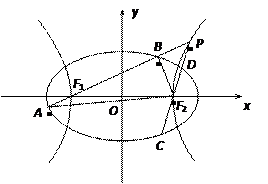
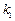 和
和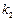 ,探求
,探求
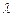 ,使得
,使得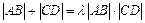 恒成立?
恒成立?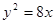 的准线与双曲线
的准线与双曲线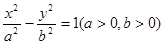 相交于A,B两点,双曲线的一条渐近线方程是
相交于A,B两点,双曲线的一条渐近线方程是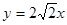 ,点F是抛物线的焦点,,且△
,点F是抛物线的焦点,,且△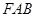 是直角三角形,则双曲线的标准方程是
是直角三角形,则双曲线的标准方程是
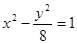
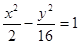
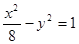
 是由双曲线
是由双曲线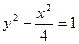 的两条渐近线和抛物线
的两条渐近线和抛物线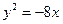 的准线所围
的准线所围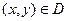 ,则目标函数
,则目标函数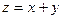 的最大值为( )
的最大值为( )



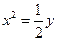 的准线方程为
的准线方程为 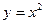 上两点
上两点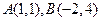 处的切线交于
处的切线交于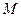 点,则
点,则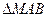 的面积为
的面积为