题目内容
由函数y=f(x)确定数列{an},an=f(n),若函数y=f(x)的反函数y=f-1(x)能确定数列{bn},bn=f-1(n),则称数列{bn}是数列{an}的“反数列”。
(1)若函数f(x)=2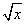 确定数列{an}的反数列为{bn},求{bn}的通项公式;
确定数列{an}的反数列为{bn},求{bn}的通项公式;
(2)对(1)中{bn},不等式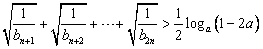 对任意的正整数n恒成立,求实数a的取值范围;
对任意的正整数n恒成立,求实数a的取值范围;
(3)设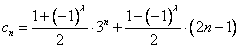 (λ为正整数),若数列{cn}的反数列为{dn},{cn}与{dn}的公共项组成的数列为{tn}, 求数列{tn}前n项和Sn。
(λ为正整数),若数列{cn}的反数列为{dn},{cn}与{dn}的公共项组成的数列为{tn}, 求数列{tn}前n项和Sn。
(1)若函数f(x)=2
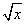 确定数列{an}的反数列为{bn},求{bn}的通项公式;
确定数列{an}的反数列为{bn},求{bn}的通项公式;(2)对(1)中{bn},不等式
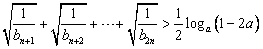 对任意的正整数n恒成立,求实数a的取值范围;
对任意的正整数n恒成立,求实数a的取值范围;(3)设
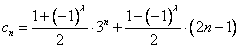 (λ为正整数),若数列{cn}的反数列为{dn},{cn}与{dn}的公共项组成的数列为{tn}, 求数列{tn}前n项和Sn。
(λ为正整数),若数列{cn}的反数列为{dn},{cn}与{dn}的公共项组成的数列为{tn}, 求数列{tn}前n项和Sn。 解:(1)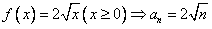 (n为正整数),
(n为正整数),
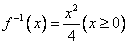 ,
,
所以数列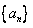 的反数列
的反数列 的通项公式
的通项公式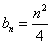 (n为正整数)。
(n为正整数)。
(2) 对于(1)中 ,不等式化为
,不等式化为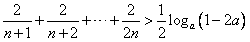 ,
,
 ,
,
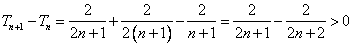 ,
,
∴数列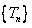 单调递增,
单调递增,
所以,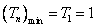 ,要使不等式恒成立,只要
,要使不等式恒成立,只要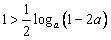 ,
,
∵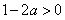 ,
,
∴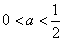 ,
,
又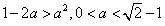 ,
,
所以,使不等式对于任意正整数n恒成立的a的取值范围是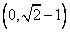 。
。
(3)设公共项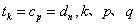 为正整数,
为正整数,
当λ为奇数时,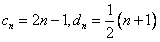 ,
,
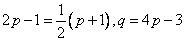 ,
,
则 (表示
(表示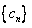 是
是 的子数列),
的子数列),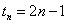 ,
,
所以,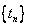 的前n项和
的前n项和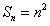 ;
;
当λ为偶数时,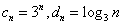 ,
,
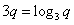 ,则
,则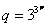 ,同样有
,同样有 ,
,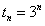 ,
,
所以,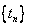 的前n项和
的前n项和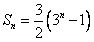 。
。
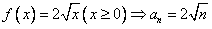 (n为正整数),
(n为正整数),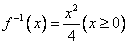 ,
,所以数列
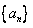 的反数列
的反数列 的通项公式
的通项公式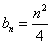 (n为正整数)。
(n为正整数)。(2) 对于(1)中
 ,不等式化为
,不等式化为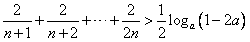 ,
, ,
,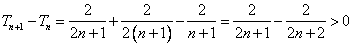 ,
,∴数列
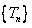 单调递增,
单调递增,所以,
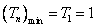 ,要使不等式恒成立,只要
,要使不等式恒成立,只要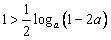 ,
,∵
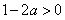 ,
,∴
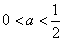 ,
,又
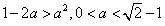 ,
,所以,使不等式对于任意正整数n恒成立的a的取值范围是
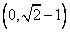 。
。(3)设公共项
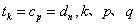 为正整数,
为正整数,当λ为奇数时,
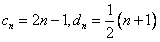 ,
,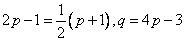 ,
,则
 (表示
(表示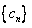 是
是 的子数列),
的子数列),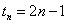 ,
,所以,
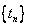 的前n项和
的前n项和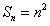 ;
;当λ为偶数时,
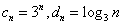 ,
,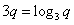 ,则
,则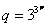 ,同样有
,同样有 ,
,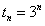 ,
,所以,
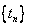 的前n项和
的前n项和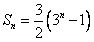 。
。
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
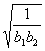 ≥1-2a对任意的正整数n恒成立,求实数a的范围;
≥1-2a对任意的正整数n恒成立,求实数a的范围;