题目内容
若函数y=f(x)存在反函数y=f-1(x),由函数y=f(x)确定数列{an},an=f(n),由函数y=f-1(x)确定数列{bn},bn=f-1(n),则称数列{bn}是数列{an}的“反数列”.
(1)若数列{bn}是函数f(x)=
确定数列{an}的反数列,试求数列{bn}的前n项和Sn;
(2)若函数f(x)=2
确定数列{cn}的反数列为{dn},求{dn}的通项公式;
(3)对(2)题中的{dn},不等式
+
+…+
>
log(1-2a)对任意的正整数n恒成立,求实数a的取值范围.
(1)若数列{bn}是函数f(x)=
| x+1 |
| 2 |
(2)若函数f(x)=2
| x |
(3)对(2)题中的{dn},不等式
|
|
|
| 1 |
| 2 |
分析:(1)由f(x)=
,知f-1(x)=2x-1,所以bn=2n-1,由此能求出Sn.
(2)由f(x)=2
,知f-1(x)=
,由此能求出{dn}的通项公式.
(3)记Tn=
+
+…+
,得Tn=
+
+…+
,故Tn+1-Tn=
-
>0,由此能求出实数a的取值范围.
| x+1 |
| 2 |
(2)由f(x)=2
| x |
| x2 |
| 4 |
(3)记Tn=
|
|
|
| 2 |
| n+1 |
| 2 |
| n+2 |
| 2 |
| 2n |
| 2 |
| 2n+1 |
| 2 |
| 2n+2 |
解答:解:(1)∵f(x)=
,
∴f-1(x)=2x-1,
所以bn=2n-1,
Sn=2(1+2+3+…+n)-n
=2×
-n=n2.(4分)
(2)∵f(x)=2
,∴f-1(x)=
,
所以dn=
.
(3)记Tn=
+
+…+
,
得Tn=
+
+…+
,
Tn+1-Tn=
-
>0,
所以{Tn}递增,故(Tn)min=T1=1.
由已知得,
loga(1-2a)<1,
解得0<a<
-1,
∴实数a的取值范围是(0,
-1).
| x+1 |
| 2 |
∴f-1(x)=2x-1,
所以bn=2n-1,
Sn=2(1+2+3+…+n)-n
=2×
| n(n+1) |
| 2 |
(2)∵f(x)=2
| x |
| x2 |
| 4 |
所以dn=
| n2 |
| 4 |
(3)记Tn=
|
|
|
得Tn=
| 2 |
| n+1 |
| 2 |
| n+2 |
| 2 |
| 2n |
Tn+1-Tn=
| 2 |
| 2n+1 |
| 2 |
| 2n+2 |
所以{Tn}递增,故(Tn)min=T1=1.
由已知得,
| 1 |
| 2 |
解得0<a<
| 2 |
∴实数a的取值范围是(0,
| 2 |
点评:本题考查数列与函数的综合应用,解题时要认真审题,仔细解答,注意反函数的合理运用,合理地进行等价转化.

练习册系列答案
相关题目
 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论: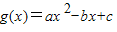 的图象与直线y=-x也一定没有交点.
的图象与直线y=-x也一定没有交点. 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论: 的图象与直线y=-x也一定没有交点.
的图象与直线y=-x也一定没有交点. 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论: 的图象与直线y=-x也一定没有交点.
的图象与直线y=-x也一定没有交点.