题目内容
非空集合 关于运算
关于运算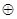 满足:(1)对任意
满足:(1)对任意 、
、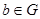 ,都有
,都有 ;(2)存在
;(2)存在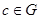 ,使得对一切
,使得对一切 ,都有
,都有 ,则称
,则称 关于运算
关于运算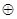 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
① {非负整数},
{非负整数},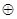 为整数的加法。
为整数的加法。
② {偶数},
{偶数},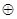 为整数的乘法。
为整数的乘法。
③ {平面向量},
{平面向量},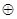 为平面向量的加法。
为平面向量的加法。
④ {二次三项式},
{二次三项式},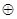 为多项式的加法。
为多项式的加法。
其中 关于运算
关于运算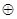 为“融洽集”的是( )
为“融洽集”的是( )
 关于运算
关于运算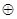 满足:(1)对任意
满足:(1)对任意 、
、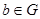 ,都有
,都有 ;(2)存在
;(2)存在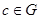 ,使得对一切
,使得对一切 ,都有
,都有 ,则称
,则称 关于运算
关于运算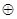 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:①
 {非负整数},
{非负整数},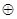 为整数的加法。
为整数的加法。②
 {偶数},
{偶数},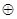 为整数的乘法。
为整数的乘法。③
 {平面向量},
{平面向量},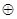 为平面向量的加法。
为平面向量的加法。④
 {二次三项式},
{二次三项式},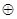 为多项式的加法。
为多项式的加法。其中
 关于运算
关于运算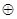 为“融洽集”的是( )
为“融洽集”的是( )| A.①② | B.①③ | C.②③ | D.②④ |
B
此题是信息类的题目,考查学生的阅读能力和自学能力,考查集合的知识点;因为非负整数加非负整数还等于非负整数,即对任意 、
、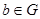 ,都有
,都有 ;当
;当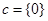 时,因为
时,因为 加任何数都等于任何数,所以满足使得对一切
加任何数都等于任何数,所以满足使得对一切 ,都有
,都有 ,所以①正确;因为平面向量的加法还是平面向量,所以对任意
,所以①正确;因为平面向量的加法还是平面向量,所以对任意 、
、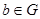 ,都有
,都有 ;当
;当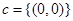 时,因为
时,因为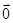 加任何向量都等于任何向量,所以满足使得对一切
加任何向量都等于任何向量,所以满足使得对一切 ,都有
,都有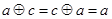 ,所以③正确;所以选B;
,所以③正确;所以选B;
 、
、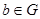 ,都有
,都有 ;当
;当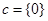 时,因为
时,因为 加任何数都等于任何数,所以满足使得对一切
加任何数都等于任何数,所以满足使得对一切 ,都有
,都有 ,所以①正确;因为平面向量的加法还是平面向量,所以对任意
,所以①正确;因为平面向量的加法还是平面向量,所以对任意 、
、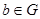 ,都有
,都有 ;当
;当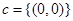 时,因为
时,因为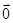 加任何向量都等于任何向量,所以满足使得对一切
加任何向量都等于任何向量,所以满足使得对一切 ,都有
,都有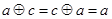 ,所以③正确;所以选B;
,所以③正确;所以选B;
练习册系列答案
相关题目
 }, 2
}, 2 A.
A. A
A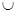 B,求
B,求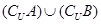 .
.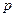 :函数
:函数 的图象与
的图象与 轴没有公共点,命题
轴没有公共点,命题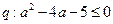 ,若命题
,若命题 为真命题,求实数
为真命题,求实数 的取值范围
的取值范围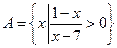 ,
,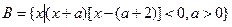
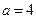 时,求
时,求
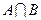 (Ⅱ)若
(Ⅱ)若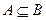 ,求实数
,求实数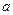 的取值范围.
的取值范围.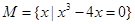 ,则M的子集个数为( )
,则M的子集个数为( ) 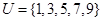 ,
,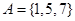 ,则
,则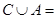 ( )
( )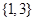
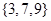
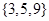
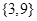
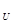 A)∩(C
A)∩(C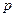 :“
:“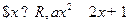 ≤0”的否定是真命题,则
≤0”的否定是真命题,则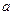 的取值范围是 .
的取值范围是 .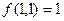 ,
,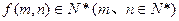 ,且对任意
,且对任意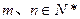 都有:
都有: ;②
;②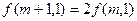 。给出以下四个结论:
。给出以下四个结论: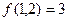 ; (2)
; (2)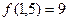 ; (3)
; (3)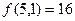 ; (4)
; (4)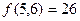 。其中正确的为______________________
。其中正确的为______________________