题目内容
设数列{an}满足a1=6，a2=4，a3=3，且数列{an+1-an}（n∈N*）是等差数列，则数列{an}的通项公式为________．
an=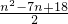
（n∈N*）
分析：先求出数列{an+1-an}（n∈N*）的首项和公差，然后求出数列{an+1-an}的通项公式，然后利用叠加法可求出数列{an}的通项公式．
解答：a2-a1=4-6=-2
a3-a2=3-4=-1
∴d=（a3-a2）-（a2-a1）=-1-（-2）=1
∵数列{an+1-an}（n∈N*）是等差数列
∴数列{an+1-an}的首项为-2，公差为1的等差数列
则an+1-an=n-3，则a2-a1=4-6=-2，a3-a2=3-4=-1，…an-an-1=n-4
相加得an=6+（-2）+（-1）+…+（n-4）=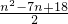
故答案为：an=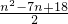（n∈N*）
点评：本题主要考查了等差数列的通项公式，以及利用叠加法求通项，同时考查了计算能力，属于中档题．
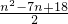（n∈N*）分析：先求出数列{an+1-an}（n∈N*）的首项和公差，然后求出数列{an+1-an}的通项公式，然后利用叠加法可求出数列{an}的通项公式．
解答：a2-a1=4-6=-2
a3-a2=3-4=-1
∴d=（a3-a2）-（a2-a1）=-1-（-2）=1
∵数列{an+1-an}（n∈N*）是等差数列
∴数列{an+1-an}的首项为-2，公差为1的等差数列
则an+1-an=n-3，则a2-a1=4-6=-2，a3-a2=3-4=-1，…an-an-1=n-4
相加得an=6+（-2）+（-1）+…+（n-4）=
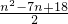
故答案为：an=
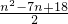（n∈N*）点评：本题主要考查了等差数列的通项公式，以及利用叠加法求通项，同时考查了计算能力，属于中档题．
练习册系列答案
相关题目
设数列{an}满足a1=1，a2+a4=6，且对任意n∈N*，函数f（x）=（an-an+1+an+2）x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
，则数列{cn}的前n项和Sn为（ ）
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|