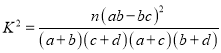题目内容
【题目】已知
是抛物线
与圆
在第一象限的公共点，其中圆心
，点
到
的焦点
的距离与
的半径相等， 
上一动点到其准线与到点
的距离之和的最小值等于
的直径， 
为坐标原点，则直线
被圆
所截得的弦长为（ ）
A. 2 B. 
C. 
D. 
【答案】D
【解析】圆心
，设半径为
， 
，据题意，由抛物线的定义可得动点到焦点
与到点
的距离之和的最小值为
，可得
三点共线时取得最小值，且有
为
的中点，由
， 
可得
，代入
的方程可得
，解得
，即有
， 
，可得点
到直线的距离为
，可得直线
被圆
所截得的弦长为，故选D．
点晴:本题考查的是圆与抛物线的综合以及直线和圆的位置关系.解决本题的关键是充分利用条件
，结合抛物线的定义可得动点到焦点
与到点
的距离之和的最小值为
，并且可得
三点共线时取得最小值，且有
为
的中点，用待定系数法可求解;直线 和圆相交求弦长要充分利用直角三角形中的勾股定理.
练习册系列答案
相关题目
【题目】为减少空气污染，某市鼓励居民用电（减少燃气或燃煤），采用分段计费的方法计算：电费每月用电不超过100度时，按每度0.57元计算；每月用电量超过100度时，其中的100度仍按原标准收费，超过的部分每度按0.5元计算.
（Ⅰ）设月用电
度时，应交电费
元，写出
关于
的函数关系式；
（Ⅱ）小明家第一季度缴纳电费情况如下：
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度？
