题目内容
已知函数 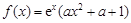
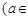 R).
R).
(Ⅰ)若
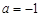 ,求曲线
,求曲线
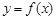 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若
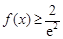 对任意
对任意 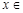
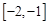 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】
(1)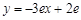 ;(2)
;(2)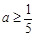
【解析】第一问中利用导数的几何意义可知当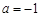 时,
时,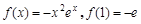 且
且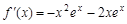 , 因为切点为(
, 因为切点为(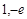 ),
则
),
则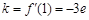 ,
,
所以在点(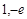 )处的曲线的切线方程为:
)处的曲线的切线方程为: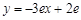
第二问中,利用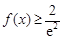 对任意
对任意 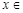
 恒成立,由题意得,
恒成立,由题意得,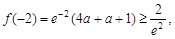 即
即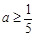 )
)
然后验证 ,
,
因为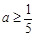 ,所以
,所以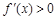 恒成立,故
恒成立,故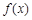 在
在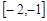 上单调递增,
上单调递增,
要使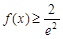 恒成立,则
恒成立,则 ,解得
,解得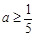
(Ⅰ)解:当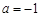 时,
时,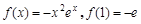 .
.
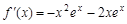 , 因为切点为(
, 因为切点为(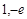 ),
则
),
则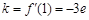 ,
,
所以在点(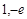 )处的曲线的切线方程为:
)处的曲线的切线方程为: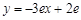 .
.
(Ⅱ)解法一:由题意得,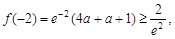 即
即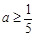 . …
. …
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为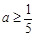 ,所以
,所以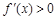 恒成立,故
恒成立,故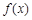 在
在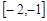 上单调递增,
上单调递增,
要使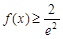 恒成立,则
恒成立,则 ,解得
,解得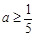
解法二:
(1)当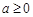 时,
时,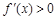 在
在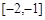 上恒成立,故
上恒成立,故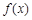 在
在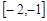 上单调递增,
上单调递增,
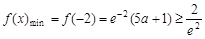 即
即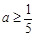 .
.
(2)当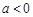 时,令
时,令 ,对称轴
,对称轴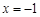 ,
,
则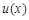 在
在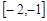 上单调递增,又
上单调递增,又
① 当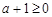 ,即
,即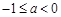 时,
时,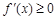 在
在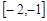 上恒成立,
上恒成立,
所以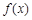 在
在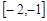 单调递增,
单调递增,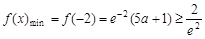 即
即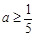 ,不合题意,舍去
,不合题意,舍去
②当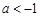 时,
时,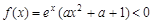 ,
不合题意,舍去 ks5综上所述:
,
不合题意,舍去 ks5综上所述: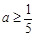

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
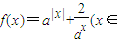 R,a>1),
R,a>1),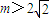 ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.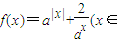 R,a>1),
R,a>1),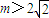 ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集. R
R ,
, 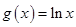
 的单调区间;
的单调区间; 的方程
的方程
 为自然对数的底数)只有一个实数根, 求
为自然对数的底数)只有一个实数根, 求 的值.
的值. R
R ,
,  .
. 的单调区间;
的单调区间; 的方程
的方程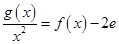
 为自然对数的底数)只有一个实数根, 求
为自然对数的底数)只有一个实数根, 求 的值.
的值. (
( ∈R).
∈R). 上具有单调性,求
上具有单调性,求