题目内容
已知函数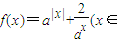 R,a>1),
R,a>1),(1)求函数f(x)的值域;
(2)记函数g(x)=f(-x),x∈[-2,+∞],若g(x)的最小值与a无关,求a的取值范围;
(3)若
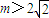 ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
【答案】分析:(1)表达式形式上提醒我们可以尝试基本不等式求解,则需要对自变量x的绝对值符号进行讨论分析.不过要注意是否真的能用基本不等式,即注意基本不等式的使用条件.
(2)本题需要通过f(x)求出g(x)表达式,观察表达式可知,解决本题的关键是对函数解析式中绝对值符合的处理,要去掉绝对值符号可以根据定义分类讨论.
(3)需要对变量m分以下两种情况讨论:
解答:解:(1)①x≥0时,∵ ,
,
当且仅当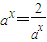 ,即
,即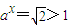 时等号成立;
时等号成立;
②x<0,∵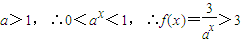 ,
,
由①②知函数f(x)的值域为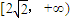 .
.
(2)g(x)=f(-x)=a|x|+2ax,x∈[-2,+∞),
①x≥0,∵a>1,∴ax≥1,g(x)=3ax,∴g(x)≥3,
②-2≤x<0时,∵ ,
,
令t=ax,则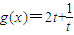 ,记
,记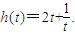
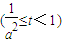 ,
,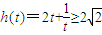 ,当且仅当
,当且仅当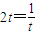 ,
,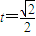 时等号成立,
时等号成立,
(i)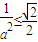 ,即
,即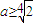 时,结合①知
时,结合①知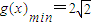 与a无关;
与a无关;
(ii)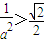 ,即
,即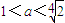 时,
时,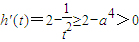 ,∴h(t)在
,∴h(t)在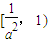 上是增函数,
上是增函数,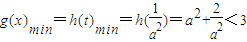 ,
,
结合①知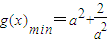 与a有关;
与a有关;
综上,若g(x)的最小值与a无关,则实数a的取值范围是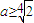 .
.
(3)①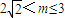 时,关于x的方程f(x)=m的解集为
时,关于x的方程f(x)=m的解集为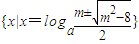 ;
;
②m>3时,关于x的方程f(x)=m的解集为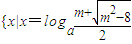 或
或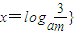 .
.
点评:(1)去绝对值符号的两种常用方法:
①绝对值定义法:|x|=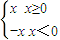
②要去绝对值式子两端同时平方.
(2)使用均值不等式的条件:
①一正(a,b都是正数);
②二定(若求a+b则ab是定值,若求ab则a+b是定值);
③三等.(当且仅当a=b时不等式取“=”).
(2)本题需要通过f(x)求出g(x)表达式,观察表达式可知,解决本题的关键是对函数解析式中绝对值符合的处理,要去掉绝对值符号可以根据定义分类讨论.
(3)需要对变量m分以下两种情况讨论:

解答:解:(1)①x≥0时,∵
 ,
,当且仅当
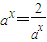 ,即
,即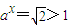 时等号成立;
时等号成立;②x<0,∵
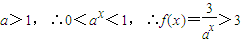 ,
,由①②知函数f(x)的值域为
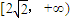 .
.(2)g(x)=f(-x)=a|x|+2ax,x∈[-2,+∞),
①x≥0,∵a>1,∴ax≥1,g(x)=3ax,∴g(x)≥3,
②-2≤x<0时,∵
 ,
,令t=ax,则
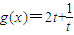 ,记
,记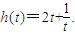
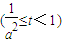 ,
,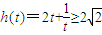 ,当且仅当
,当且仅当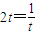 ,
,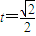 时等号成立,
时等号成立,(i)
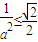 ,即
,即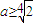 时,结合①知
时,结合①知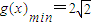 与a无关;
与a无关;(ii)
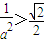 ,即
,即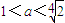 时,
时,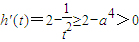 ,∴h(t)在
,∴h(t)在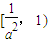 上是增函数,
上是增函数,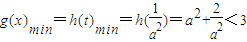 ,
,结合①知
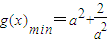 与a有关;
与a有关;综上,若g(x)的最小值与a无关,则实数a的取值范围是
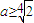 .
.(3)①
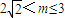 时,关于x的方程f(x)=m的解集为
时,关于x的方程f(x)=m的解集为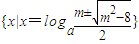 ;
;②m>3时,关于x的方程f(x)=m的解集为
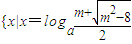 或
或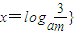 .
.点评:(1)去绝对值符号的两种常用方法:
①绝对值定义法:|x|=
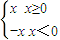
②要去绝对值式子两端同时平方.
(2)使用均值不等式的条件:
①一正(a,b都是正数);
②二定(若求a+b则ab是定值,若求ab则a+b是定值);
③三等.(当且仅当a=b时不等式取“=”).

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
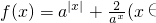 R,a>1),
R,a>1), ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.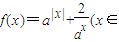 R,a>1),
R,a>1), ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.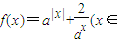 R,a>1),
R,a>1),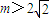 ,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.
,直接写出(不需给出演算步骤)关于x的方程f(x)=m的解集.