题目内容
设函数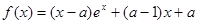 ,
,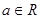 。
。
(1)当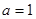 时,求
时,求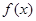 的单调区间;
的单调区间;
(2)(i)设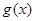 是
是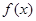 的导函数,证明:当
的导函数,证明:当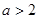 时,在
时,在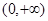 上恰有一个
上恰有一个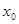 使得
使得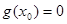 ;
;
(ii)求实数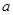 的取值范围,使得对任意的
的取值范围,使得对任意的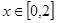 ,恒有
,恒有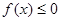 成立。
成立。
注: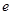 为自然对数的底数。
为自然对数的底数。
(1)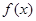 的减区间是
的减区间是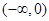 ;增区间是
;增区间是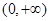
(2)在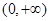 上恰有一个
上恰有一个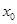 使得
使得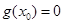 .
.
(ⅱ)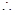
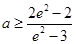 。
。
解析试题分析:(1)当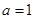 时,
时,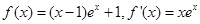 1分
1分
当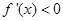 时,
时,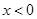 ;当
;当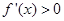 时,
时,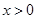
所以函数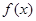 的减区间是
的减区间是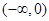 ;增区间是
;增区间是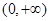 3分
3分
(2)(ⅰ)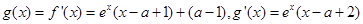 4分
4分
当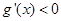 时,
时,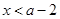 ;当
;当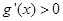 时,
时,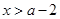
因为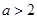 ,所以函数
,所以函数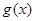 在
在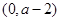 上递减;在
上递减;在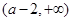 上递增 6分
上递增 6分
又因为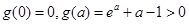 ,
,
所以在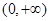 上恰有一个
上恰有一个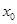 使得
使得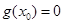 . 8分
. 8分
(ⅱ)若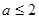 ,可得在
,可得在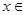
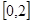 时,
时,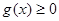 ,从而
,从而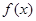 在
在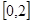 内单调递增,而
内单调递增,而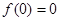 ,
,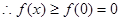 ,不符题意。
,不符题意。 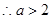
由(ⅰ)知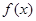 在
在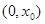 递减,
递减,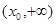 递增,
递增,
设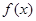 在
在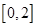 上最大值为
上最大值为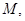 则
则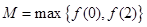 ,
,
若对任意的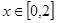 ,恒有
,恒有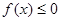 成立,则
成立,则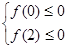 , 11分
, 11分
由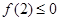 得
得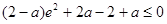 ,
,
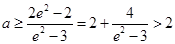 ,
,
又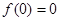 ,
,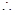
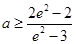 。 13
。 13
考点:本题主要考查应用导数研究函数的单调性、最值,恒成立问题。
点评:典型题,本题属于导数应用中的基本问题,首先通过求导数,研究导数值的正负情况,确定函数单调区间。应用同样的方法,研究函数图象的形态,明确方程解的情况。作为“恒成立问题”往往转化成求函数的最值。

练习册系列答案
相关题目
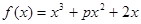 (常数
(常数 )在
)在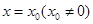 处取得极大值M=0.
处取得极大值M=0.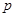 的值;
的值;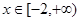 ,方程
,方程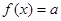 有解,求
有解,求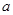 的取值范围.
的取值范围.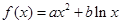 ,其中
,其中 .证明:当
.证明:当 时,函数
时,函数 没有极值点;当
没有极值点;当 时,函数
时,函数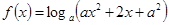 在
在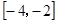 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.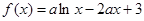 (
(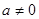 ).
). 的单调区间;
的单调区间;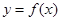 的图像在
的图像在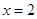 处的切线的斜率为
处的切线的斜率为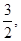 若函数
若函数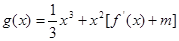 ,在区间(1,3)上不是单调函数,求
,在区间(1,3)上不是单调函数,求  的取值范围。
的取值范围。 =
= ,数列
,数列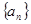 满足
满足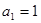 ,
,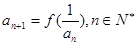 。(12分)
。(12分)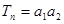 -
-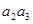 +
+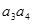 -
-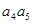 +…+
+…+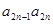 -
-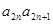 求
求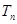 ;
;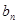 =
=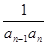 (
(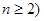 ,
,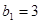 ,
,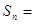
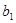 +
+ +
+ +┅
+┅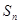 <
<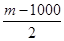 对一切
对一切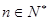 都成立,求最小的正整数
都成立,求最小的正整数 。
。
 的单调区间;
的单调区间; 在
在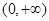 内恒成立,求实数a的取值范围;
内恒成立,求实数a的取值范围; ,求证:
,求证:
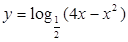
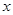 满足
满足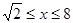 ,求函数
,求函数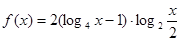 的最大值和最小值
的最大值和最小值