题目内容
已知函数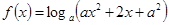 在
在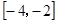 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
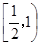
解析试题分析:(1)当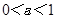 时,函数
时,函数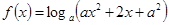 在
在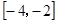 上是增函数
上是增函数 函数
函数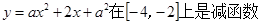
 抛物线对称轴
抛物线对称轴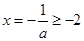
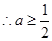 即
即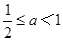
(2)当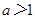 时,函数
时,函数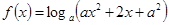 在
在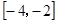 上是增函数
上是增函数

 抛物线对称轴
抛物线对称轴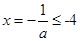
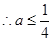 即
即
综上所述a的取值范围是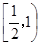
考点:本题主要考查复合的手术刀性质,二次函数的图象和性质。
点评:对数函数的单调性,取决于底数与1 的大小比较。复合函数的单调性遵循“内外层函数,同增异减”。特别注意函数定义域,对数真数大于0.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
题目内容
已知函数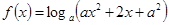 在
在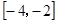 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
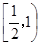
解析试题分析:(1)当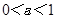 时,函数
时,函数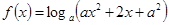 在
在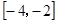 上是增函数
上是增函数 函数
函数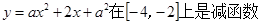
 抛物线对称轴
抛物线对称轴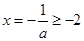
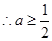 即
即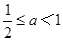
(2)当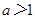 时,函数
时,函数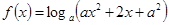 在
在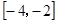 上是增函数
上是增函数

 抛物线对称轴
抛物线对称轴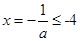
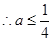 即
即
综上所述a的取值范围是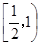
考点:本题主要考查复合的手术刀性质,二次函数的图象和性质。
点评:对数函数的单调性,取决于底数与1 的大小比较。复合函数的单调性遵循“内外层函数,同增异减”。特别注意函数定义域,对数真数大于0.

 全程金卷系列答案
全程金卷系列答案