��Ŀ����
��֪������{an}��a1=a��a2=p������p��0�����������������n��Sn=a1+a2+��+an������Sn����Sn=
��
��1����a��ֵ��
��2����ȷ������{an}�Dz��ǵȲ����У����ǣ������ͨ�ʽ�������ǣ�˵�����ɣ�
��3����pn=
+
���Ƿ����������M��ʹ����ʽp1+p2+��+pn-2n��M������������ڣ����M����Сֵ���������ڣ�˵�����ɣ�
| n(an-a1) |
| 2 |
��1����a��ֵ��
��2����ȷ������{an}�Dz��ǵȲ����У����ǣ������ͨ�ʽ�������ǣ�˵�����ɣ�
��3����pn=
| Sn+2 |
| Sn+1 |
| Sn+1 |
| Sn+2 |
��������1���� a=a1=s1 �� Sn=
�ɵ� a ��ֵ��
��2������� Sn���ɵ� Sn-1������Sn-Sn-1=an������ɵ�
=
��an =k��n-1����������{an}�ǵȲ����У���a2 =p=k•��2-1������� k ֵ���õ�an =p��n-1��=��n-1��p��
��3�����ݶ����ȱ�ʾ��p1+p2+��+pn-2n=2+1-
-
���������ϱ߽缴�ɣ�
| n(an-a1) |
| 2 |
��2������� Sn���ɵ� Sn-1������Sn-Sn-1=an������ɵ�
| an |
| an-1 |
| n-1 |
| n-2 |
��3�����ݶ����ȱ�ʾ��p1+p2+��+pn-2n=2+1-
| 2 |
| n+1 |
| 2 |
| n+2 |
����⣺��1������֪����s1=
=a1=a����a=0
��2����a1=0��Sn=
����Sn+1=
��
��2��Sn+1-Sn��=��n+1��an+1-nan����2an+1=��n+1��an+1-nan��
������n-1��an+1=nan��������nan+2=��n+1��an+1��
��nan+2-��n-1��an+1=��n+1��an+1-nan����n��an+2-an+1��=n��an+1-an����
��n�����������������n��N����an+2-an+1=an+1-an��
������{an}�ǵȲ����У���ͨ�ʽ��an=��n-1��p��
��3����Sn=
��pn=
+
=2+
-
��p1+p2+p3+��+pn-2n=(2+
-
)+(2+
-
)+��+(2+
-
)-2n
=2+1-
-
��
��n���������ɵ�p1+p2+��+pn-2n��3��
�ʴ�����С��������M=3��ʹ����ʽp1+p2+��+pn-2n��M�������
| 1•(a-a) |
| 2 |
��2����a1=0��Sn=
| nan |
| 2 |
| (n+1)an+1 |
| 2 |
��2��Sn+1-Sn��=��n+1��an+1-nan����2an+1=��n+1��an+1-nan��
������n-1��an+1=nan��������nan+2=��n+1��an+1��
��nan+2-��n-1��an+1=��n+1��an+1-nan����n��an+2-an+1��=n��an+1-an����
��n�����������������n��N����an+2-an+1=an+1-an��
������{an}�ǵȲ����У���ͨ�ʽ��an=��n-1��p��
��3����Sn=
| n(n-1)p |
| 2 |
| ||
|
| ||
|
| 2 |
| n |
| 2 |
| n+2 |
��p1+p2+p3+��+pn-2n=(2+
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
| 4 |
| 2 |
| n |
| 2 |
| n+2 |
=2+1-
| 2 |
| n+1 |
| 2 |
| n+2 |
��n���������ɵ�p1+p2+��+pn-2n��3��
�ʴ�����С��������M=3��ʹ����ʽp1+p2+��+pn-2n��M�������
���������⿼�����е��ۺ����⣬�������еĵ��ƹ�ϵ��ͨ�ʽ֮��Ĺ�ϵ������ѧ��̽��������Ľ��������ע������ת���뻯��˼������ã�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��
��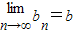 �����bΪ����{bn}�ġ��Ͻ���ֵ������
�����bΪ����{bn}�ġ��Ͻ���ֵ������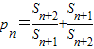 ��������{p1+p2+��+pn-2n}�ġ��Ͻ���ֵ����
��������{p1+p2+��+pn-2n}�ġ��Ͻ���ֵ����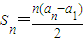 ��
��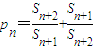 ���Ƿ����������M��ʹ����ʽp1+p2+��+pn-2n��M������������ڣ����M����Сֵ���������ڣ�˵�����ɣ�
���Ƿ����������M��ʹ����ʽp1+p2+��+pn-2n��M������������ڣ����M����Сֵ���������ڣ�˵�����ɣ�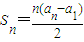 ��
��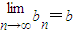 �����bΪ����{bn}�ġ��Ͻ���ֵ������
�����bΪ����{bn}�ġ��Ͻ���ֵ������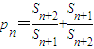 ��������{p1+p2+��+pn-2n}�ġ��Ͻ���ֵ����
��������{p1+p2+��+pn-2n}�ġ��Ͻ���ֵ����