题目内容
已知,数列{an}有a1=a,a2=p(常数p>0),对任意的正整数n,Sn=a1+a2+…+an,并有Sn满足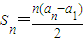 .
.(1)求a的值;
(2)试确定数列{an}是不是等差数列,若是,求出其通项公式.若不是,说明理由;
(3)令
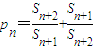 ,是否存在正整数M,使不等式p1+p2+…+pn-2n≤M恒成立,若存在,求出M的最小值,若不存在,说明理由.
,是否存在正整数M,使不等式p1+p2+…+pn-2n≤M恒成立,若存在,求出M的最小值,若不存在,说明理由.
【答案】分析:(1)由 a=a1=s1 和 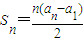 可得 a 的值.
可得 a 的值.
(2)先求出 Sn,可得 Sn-1,根据Sn-Sn-1=an,化简可得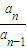 =
=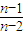 ,an =k(n-1),故数列{an}是等差数列.由a2 =p=k•(2-1),求出 k 值,得到an =p(n-1)=(n-1)p.
,an =k(n-1),故数列{an}是等差数列.由a2 =p=k•(2-1),求出 k 值,得到an =p(n-1)=(n-1)p.
(3)根据定义先表示出p1+p2+…+pn-2n=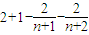 ,再求其上边界即可.
,再求其上边界即可.
解答:解:(1)由已知,得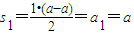 ,∴a=0
,∴a=0
(2)由a1=0得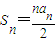 ,则
,则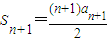 ,
,
∴2(Sn+1-Sn)=(n+1)an+1-nan,即2an+1=(n+1)an+1-nan,
于是有(n-1)an+1=nan,并且有nan+2=(n+1)an+1,
∴nan+2-(n-1)an+1=(n+1)an+1-nan,即n(an+2-an+1)=n(an+1-an),
而n是正整数,则对任意n∈N都有an+2-an+1=an+1-an,
∴数列{an}是等差数列,其通项公式是an=(n-1)p.
(3)∵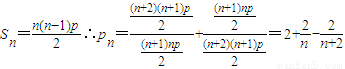
∴p1+p2+p3+…+pn-2n=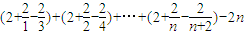
=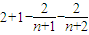 ;
;
由n是正整数可得p1+p2+…+pn-2n<3,
故存在最小的正整数M=3,使不等式p1+p2+…+pn-2n≤M恒成立.
点评:本题考查数列的综合问题,考查数列的递推关系与通项公式之间的关系,考查学生探究性问题的解决方法,注意体现转化与化归思想的运用.
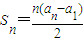 可得 a 的值.
可得 a 的值.(2)先求出 Sn,可得 Sn-1,根据Sn-Sn-1=an,化简可得
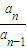 =
=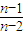 ,an =k(n-1),故数列{an}是等差数列.由a2 =p=k•(2-1),求出 k 值,得到an =p(n-1)=(n-1)p.
,an =k(n-1),故数列{an}是等差数列.由a2 =p=k•(2-1),求出 k 值,得到an =p(n-1)=(n-1)p.(3)根据定义先表示出p1+p2+…+pn-2n=
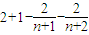 ,再求其上边界即可.
,再求其上边界即可.解答:解:(1)由已知,得
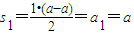 ,∴a=0
,∴a=0(2)由a1=0得
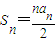 ,则
,则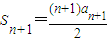 ,
,∴2(Sn+1-Sn)=(n+1)an+1-nan,即2an+1=(n+1)an+1-nan,
于是有(n-1)an+1=nan,并且有nan+2=(n+1)an+1,
∴nan+2-(n-1)an+1=(n+1)an+1-nan,即n(an+2-an+1)=n(an+1-an),
而n是正整数,则对任意n∈N都有an+2-an+1=an+1-an,
∴数列{an}是等差数列,其通项公式是an=(n-1)p.
(3)∵
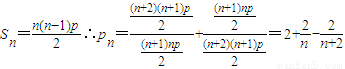
∴p1+p2+p3+…+pn-2n=
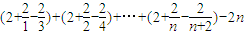
=
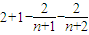 ;
;由n是正整数可得p1+p2+…+pn-2n<3,
故存在最小的正整数M=3,使不等式p1+p2+…+pn-2n≤M恒成立.
点评:本题考查数列的综合问题,考查数列的递推关系与通项公式之间的关系,考查学生探究性问题的解决方法,注意体现转化与化归思想的运用.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 .
.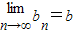 ,则称b为数列{bn}的“上渐进值”,令
,则称b为数列{bn}的“上渐进值”,令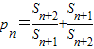 ,求数列{p1+p2+…+pn-2n}的“上渐进值”.
,求数列{p1+p2+…+pn-2n}的“上渐进值”.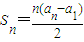 .
.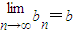 ,则称b为数列{bn}的“上渐进值”,令
,则称b为数列{bn}的“上渐进值”,令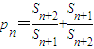 ,求数列{p1+p2+…+pn-2n}的“上渐进值”.
,求数列{p1+p2+…+pn-2n}的“上渐进值”.