题目内容
已知,数列{an}有a1=a,a2=2,对任意的正整数n,Sn=a1+a2+…+an,并有Sn满足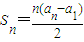 .
.(1)求a的值;
(2)求证数列{an}是等差数列;
(3)对于数列{bn},假如存在一个常数b使得对任意的正整数n都有bn<b且
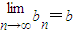 ,则称b为数列{bn}的“上渐进值”,令
,则称b为数列{bn}的“上渐进值”,令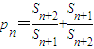 ,求数列{p1+p2+…+pn-2n}的“上渐进值”.
,求数列{p1+p2+…+pn-2n}的“上渐进值”.
【答案】分析:(1)利用s1=a1,分别代入可求a的值;
(2)欲证数列{an}是等差数列,只需证明an+2-an+1=an+1-an,利用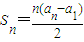 可证;
可证;
(3)根据定义先表示出p1+p2+…+pn-2n=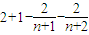 ,再求其极限即可.
,再求其极限即可.
解答:解:(1)由已知,得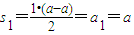 ,∴a=0…(4分)
,∴a=0…(4分)
(2)由a1=0得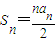 ,则
,则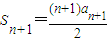 ,
,
∴2(Sn+1-Sn)=(n+1)an+1-nan,即2an+1=(n+1)an+1-nan,
于是有(n-1)an+1=nan,并且有nan+2=(n+1)an+1,
∴nan+2-(n-1)an+1=(n+1)an+1-nan,即n(an+2-an+1)=n(an+1-an),
而n是正整数,则对任意n∈N都有an+2-an+1=an+1-an,
∴数列{an}是等差数列,其通项公式是an=2(n-1).…(10分)
(3)∵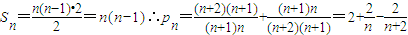
∴p1+p2+p3+…+pn-2n=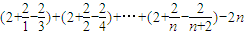 =
=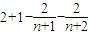 ;由n是正整数可得p1+p2+…+pn-2n<3,
;由n是正整数可得p1+p2+…+pn-2n<3,
并且有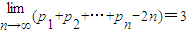 ,
,
∴数列{p1+p2+…+pn-2n}的“上渐进值”等于3.…(18分)
点评:本题的考点是等差数列的确定,考查数列的综合问题,考查数列的递推关系与通项公式之间的关系,考查学生探究性问题的解决方法,注意体现转化与化归思想的运用,考查学生分析问题解决问题的能力和意识.
(2)欲证数列{an}是等差数列,只需证明an+2-an+1=an+1-an,利用
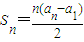 可证;
可证;(3)根据定义先表示出p1+p2+…+pn-2n=
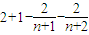 ,再求其极限即可.
,再求其极限即可.解答:解:(1)由已知,得
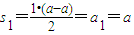 ,∴a=0…(4分)
,∴a=0…(4分)(2)由a1=0得
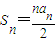 ,则
,则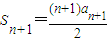 ,
,∴2(Sn+1-Sn)=(n+1)an+1-nan,即2an+1=(n+1)an+1-nan,
于是有(n-1)an+1=nan,并且有nan+2=(n+1)an+1,
∴nan+2-(n-1)an+1=(n+1)an+1-nan,即n(an+2-an+1)=n(an+1-an),
而n是正整数,则对任意n∈N都有an+2-an+1=an+1-an,
∴数列{an}是等差数列,其通项公式是an=2(n-1).…(10分)
(3)∵
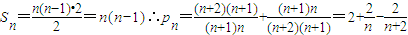
∴p1+p2+p3+…+pn-2n=
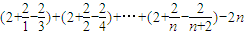 =
=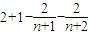 ;由n是正整数可得p1+p2+…+pn-2n<3,
;由n是正整数可得p1+p2+…+pn-2n<3,并且有
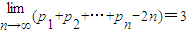 ,
,∴数列{p1+p2+…+pn-2n}的“上渐进值”等于3.…(18分)
点评:本题的考点是等差数列的确定,考查数列的综合问题,考查数列的递推关系与通项公式之间的关系,考查学生探究性问题的解决方法,注意体现转化与化归思想的运用,考查学生分析问题解决问题的能力和意识.

练习册系列答案
相关题目
 .
.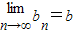 ,则称b为数列{bn}的“上渐进值”,令
,则称b为数列{bn}的“上渐进值”,令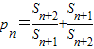 ,求数列{p1+p2+…+pn-2n}的“上渐进值”.
,求数列{p1+p2+…+pn-2n}的“上渐进值”.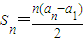 .
.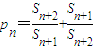 ,是否存在正整数M,使不等式p1+p2+…+pn-2n≤M恒成立,若存在,求出M的最小值,若不存在,说明理由.
,是否存在正整数M,使不等式p1+p2+…+pn-2n≤M恒成立,若存在,求出M的最小值,若不存在,说明理由.