题目内容
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合). 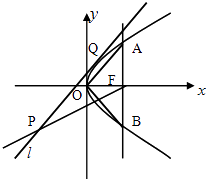
(1)求抛物线C的方程;
(2)若以线段PQ为直径的圆恰好经过F,求|PF|的最小值.
【答案】
(1)解:由已知可得:F的坐标为 ![]() ,|AB|=2p,
,|AB|=2p,
∴ ![]() ,
,
∴p=4,
∴抛物线方程为y2=8x;
(2)解:设Q(x0,y0),P(x1,y1)
设直线为l:y﹣y0=k(x﹣x0),联立方程 ![]() 得
得 ![]()
利用△=0化简可得: ![]() ,
,
又∵ ![]() ,可得
,可得 ![]()
∴直线l:y0y=4(x+x0),
∵ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∵y1y0=4(x0+x1),
∴x1x0+2(x0+x1)+4=(x1+2)(x0+2)=0,
∵x0>0,
∴x1+2=0,
∴x1=﹣2,
即点P是抛物线准线x=﹣2上的点
∴PF的最小值是4
【解析】(1)F的坐标为 ![]() ,根据三角形的面积即可求出p的值,问题得以解决;(2)设Q(x0 , y0),P(x1 , y1)设直线为l:y﹣y0=k(x﹣x0),根据韦达定理求出和向量的数量积的运算,即可求出x1的值,问题得以解决.
,根据三角形的面积即可求出p的值,问题得以解决;(2)设Q(x0 , y0),P(x1 , y1)设直线为l:y﹣y0=k(x﹣x0),根据韦达定理求出和向量的数量积的运算,即可求出x1的值,问题得以解决.

练习册系列答案
相关题目