题目内容
.已知a,b∈R,若关于x的方程x2-ax+b=0的实根x1和x2满足-1≤x1≤1,1≤x2≤2,则在平面直角坐标系aOb中,点(a,b)所表示的区域内的点P到曲线(a+3)2+(b-2)2=1上的点Q的距离|PQ|的最小值为( )
A、3
| ||
B、2
| ||
C、3
| ||
D、2
|
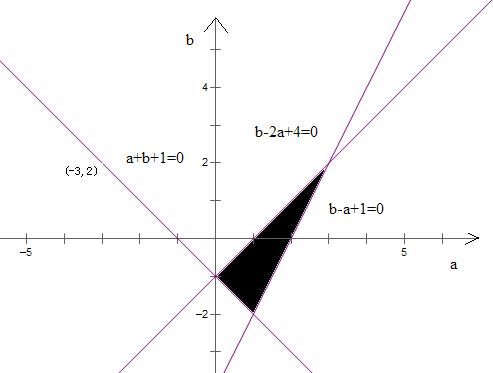
分析:先由根的分布得出关于a,b的方程组,作出方程组对应的区域,即点(a,b)所表示的区域,点P到曲线(a+3)2+(b-2)2=1上的点Q的距离|PQ|的最小值即区域内的点到定点(-3,2)的距离的最小值.由图象判断找出两点中距离最近的点,用两点距离公式求出即可.
解答:解:由题意可得
其对应的区域如图所示阴影部分,曲线(a+3)2+(b-2)2=1的圆心为(-3,2),此点在直线a+b+1=0上,由于两直线a+b+1=0与1-a+b=0垂直,故圆心与区域边界处的点(0,-1)距离是区域中的点与圆心的距离的最小值,其长度为3
,故点(a,b)所表示的区域内的点P到曲线(a+3)2+(b-2)2=1上的点Q的距离|PQ|的最小值为3
-1,
故选A.
|
| 2 |
| 2 |
故选A.

点评:本题考查简单线性规划,是线性规划求最值的一个变形题---两个动点之间的距离,动中有静,根据圆的几何特征,将两动点之间的距离转化为定点之间的距离.这是数学中常用的转化方法.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目