题目内容
选做题
(1)已知a,b∈R,若M=
所对应的变换TM把直线L:2x-y=3变换为自身,求实数a,b,并求M的逆矩阵.
(2)已知直线l的参数方程为
(t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-
).
(Ⅰ)求直线l的倾斜角;
(Ⅱ)若直线l与曲线C交于A,B两点,求|AB|.
(1)已知a,b∈R,若M=
|
(2)已知直线l的参数方程为
|
| π |
| 4 |
(Ⅰ)求直线l的倾斜角;
(Ⅱ)若直线l与曲线C交于A,B两点,求|AB|.
分析:(1)首先分析题目已知M=
对应的变换TM把直线L:2x-y=3变换为自身,故可根据变换的性质列出一组方程式求解出a,b即可得到矩阵M,再根据MM1=E,求得M的逆矩阵即可.
(2)(Ⅰ)把直线l的参数方程化为普通方程,根据直线的斜率,求出倾斜角的值.把曲线C的极坐标方程化为直角坐标方程,利用点到直线的距离公式求出圆心到直线的距离d,再由弦长公式求出AB的值
|
(2)(Ⅰ)把直线l的参数方程化为普通方程,根据直线的斜率,求出倾斜角的值.把曲线C的极坐标方程化为直角坐标方程,利用点到直线的距离公式求出圆心到直线的距离d,再由弦长公式求出AB的值
解答:解:(1)设P(x,y)为直线2x-y=3上任意一点其在M的作用下变为(x',y'),
则
=
=
,∴
.
代入2x-y=3得:-(b+2)x+(2a-3)y=3,其与2x-y=3完全一样.
∴
,解得
,则M=
.
又因为MM1=E,∴M-1=
.
(2)(Ⅰ)把直线l的参数方程
(t为参数),化为普通方程为y=
x+
,
它的斜率为
,故它的倾斜角等于60°.
(Ⅱ)由于l的直角坐标方程为y=
x+
,即
x-y+
=0.
曲线C的极坐标方程ρ=2cos(θ-
),即 ρ2=2ρ(
cosθ+
sinθ),
∴x2+y2=
x+
y,即 (x-
)2+(y-
)2=1.
故圆心 (
,
)到直线的距离d=
=
,
故弦长AB=2
=
.
则
|
|
|
|
|
代入2x-y=3得:-(b+2)x+(2a-3)y=3,其与2x-y=3完全一样.
∴
|
|
|
又因为MM1=E,∴M-1=
|
(2)(Ⅰ)把直线l的参数方程
|
| 3 |
| ||
| 2 |
它的斜率为
| 3 |
(Ⅱ)由于l的直角坐标方程为y=
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
曲线C的极坐标方程ρ=2cos(θ-
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
∴x2+y2=
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
故圆心 (
| ||
| 2 |
| ||
| 2 |
|
| ||||||||||||||
|
| ||
| 4 |
故弦长AB=2
| r2- d 2 |
| ||
| 2 |
点评:此题主要考查矩阵变换的问题,其中涉及到逆矩阵的求法.把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 使
使 成立,则实数
成立,则实数 的取值集合是__________.
的取值集合是__________. ,则线段CD的长为________.
,则线段CD的长为________.
 :
: (t为参数)与圆C2:
(t为参数)与圆C2: (
( 为参数)的位置关系不可能是________.
为参数)的位置关系不可能是________. 使
使 成立,则实数
成立,则实数 的取值集合是__________.
的取值集合是__________. ,则线段CD的长为________.
,则线段CD的长为________.
 :
: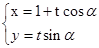 (t为参数)与圆C2:
(t为参数)与圆C2: (
( 为参数)的位置关系不可能是________.
为参数)的位置关系不可能是________.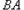 的A长线交于
的A长线交于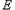 点。
点。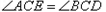 ;
;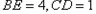 ,求
,求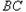 的长
的长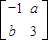 所对应的变换TM把直线L:2x-y=3变换为自身,求实数a,b,并求M的逆矩阵.
所对应的变换TM把直线L:2x-y=3变换为自身,求实数a,b,并求M的逆矩阵. (t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-
(t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-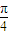 ).
).