题目内容
选修4-2：（矩阵与变换）已知a，b∈R，若矩阵M=
|
分析：因为矩阵M=
所对应的变换把直线l：2x-y=3变换为自身，也就是说直线l上的点经过变换后没有变，我们可以任取直线l上的两点，对其进行变换列出两个方程，通过解方程求得a，b的值．
|
解答：解：（方法一）在直线l上取两点（
，0），（0，-3）．
因为
=
，
=
，…（6分）
因为M对应的变换把直线变换为自身，所以点（-
，
b），（-3a，-9）仍在直线l上．
代入直线方程得
解得
…（10分）
（方法二）设（x，y）为直线l上任意一点，则
=
，…（3分）
因为M对应的变换把直线变换为自身，所以点（-x+ay，bx+3y）仍在直线l上，
代入直线方程得：2（-x+ay）-（bx+3y）=3，…（7分）
化简得（-2-b）x+（2a-3）y=3，又直线l：2x-y=3，
所以
解得
…（10分）
| 3 |
| 2 |
因为
|
|
|
|
|
|
因为M对应的变换把直线变换为自身，所以点（-
| 3 |
| 2 |
| 3 |
| 2 |
代入直线方程得
|
|
（方法二）设（x，y）为直线l上任意一点，则
|
|
|
因为M对应的变换把直线变换为自身，所以点（-x+ay，bx+3y）仍在直线l上，
代入直线方程得：2（-x+ay）-（bx+3y）=3，…（7分）
化简得（-2-b）x+（2a-3）y=3，又直线l：2x-y=3，
所以
|
|
点评：此题考查在特殊变换下的不变直线，我们可以根据特殊值法进行求解，是非常方便的，这也是高考中常用的方法．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．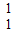
]，并且矩阵M对应的变换将点（-1，2）变换成（9，15），求矩阵M．
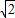sin（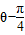
），以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
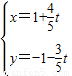（t为参数），求直线l被曲线C所截得的弦长．
所对应的变换把直线l：2x-y=3变换为自身，求a，b的值．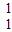
]，并且矩阵M对应的变换将点（-1，2）变换成（9，15），求矩阵M．
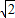sin（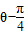
），以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
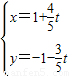（t为参数），求直线l被曲线C所截得的弦长．