题目内容
在直角坐标系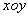 中,曲线
中,曲线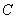 的参数方程为
的参数方程为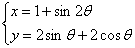 (
(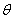 为参数)。
为参数)。
若以直角坐标系的原点为极点,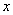 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线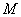 的极坐标方程为
的极坐标方程为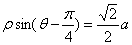 (其中
(其中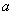 为常数)
为常数)
(1)当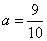 时,曲线
时,曲线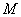 与曲线
与曲线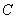 有两个交点
有两个交点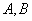 .求
.求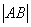 的值;
的值;
(2)若曲线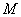 与曲线
与曲线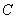 只有一个公共点,求
只有一个公共点,求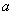 的取值范围.
的取值范围.
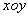 中,曲线
中,曲线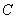 的参数方程为
的参数方程为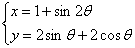 (
(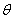 为参数)。
为参数)。若以直角坐标系的原点为极点,
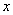 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线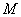 的极坐标方程为
的极坐标方程为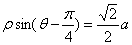 (其中
(其中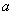 为常数)
为常数)(1)当
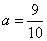 时,曲线
时,曲线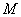 与曲线
与曲线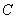 有两个交点
有两个交点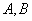 .求
.求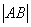 的值;
的值;(2)若曲线
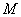 与曲线
与曲线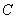 只有一个公共点,求
只有一个公共点,求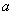 的取值范围.
的取值范围.(1)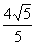 (2)
(2)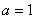 或
或 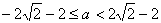
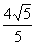 (2)
(2)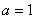 或
或 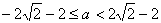
试题分析:
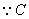 的方程是
的方程是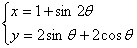 ,消去参数
,消去参数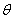 ,得
,得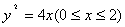
曲线
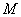 的方程
的方程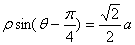 即
即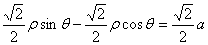
转化为直角坐标方程为:
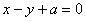 .
. (1)当
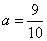 时,联立
时,联立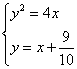 ,化简得:
,化简得: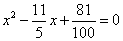
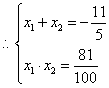
即
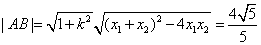
(2)曲线
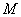 与曲线
与曲线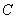 只有一个交点,?相切时,将
只有一个交点,?相切时,将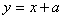 代入
代入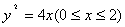 得
得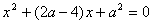 只有一个解
只有一个解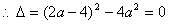 得
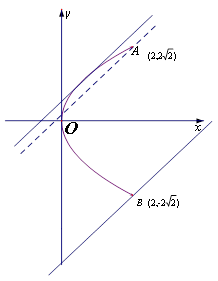
得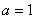 ?相交时,如图:
?相交时,如图: 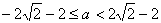 综上:曲线
综上:曲线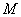 与曲线
与曲线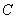 只有一个交点时
只有一个交点时 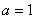 或
或 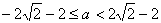
点评:此题考查学生会将圆的方程化为普通方程,掌握余弦函数的图象和性质,灵活运用韦达定理化简求值,是一道综合题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
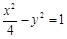 的渐近线与圆
的渐近线与圆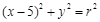 (
(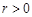 )相切,则
)相切,则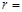
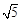
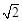
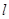 的参数方程为
的参数方程为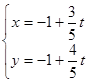 (
(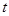 为参数).若以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
为参数).若以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为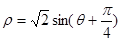 .
.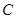 所截得的弦长.
所截得的弦长.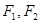 分别为双曲线
分别为双曲线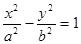 的左右焦点,点P在双曲线的右支上,且
的左右焦点,点P在双曲线的右支上,且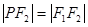 ,
,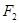 到直线
到直线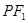 的距离等于双曲线的实轴长,则该双曲线的离心率为( )
的距离等于双曲线的实轴长,则该双曲线的离心率为( )
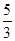
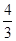
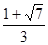
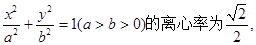 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=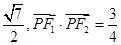 (O为坐标原点)。
(O为坐标原点)。 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。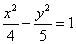 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则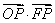 的最小值为( )
的最小值为( )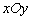 有相同的长度单位,以原点
有相同的长度单位,以原点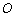 为极点,以
为极点,以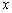 正半轴为极轴,已知曲线
正半轴为极轴,已知曲线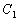 的极坐标方程为
的极坐标方程为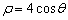 ,曲线
,曲线 的参数方程是
的参数方程是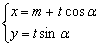 (
(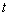 为参数,
为参数,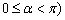 ,射线
,射线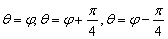 与曲线
与曲线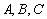
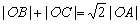 ;
;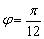 时,
时,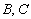 两点在曲线
两点在曲线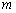 与
与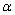 的值.
的值.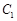 的极坐标方程是
的极坐标方程是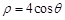 ,以极点为原点,极轴为
,以极点为原点,极轴为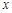 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: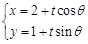 (为参数).
(为参数).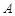 ,
,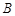 两点,点
两点,点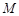 的直角坐标为
的直角坐标为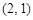 ,若
,若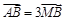 ,求直线的普通方程.
,求直线的普通方程.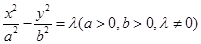 同一条渐近线上的两个不同的点,已知向量
同一条渐近线上的两个不同的点,已知向量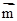 =(1,0),
=(1,0),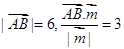 ,则双曲线的离心率e等于
,则双曲线的离心率e等于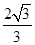 C.2或
C.2或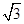 D. 2或
D. 2或