题目内容
20.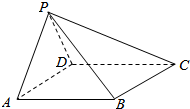 如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.
如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.(Ⅰ)求证:PB⊥AD;
(Ⅱ)若PB=$\sqrt{6}$,求点C到平面PBD的距离.
分析 (Ⅰ)取AD的中点O,连接OP,OB,证明AD⊥平面OPB,即可证明PB⊥AD;
(Ⅱ)证明OP⊥平面CBD,利用等体积求点C到平面PBD的距离.
解答 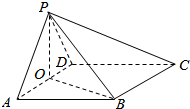 (Ⅰ)证明:取AD的中点O,连接OP,OB,则
(Ⅰ)证明:取AD的中点O,连接OP,OB,则
∵四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA,∠BAD=60°,
∴OP⊥AD,OB⊥AD,
∵OP∩OB=O,
∴AD⊥平面OPB,
∵PB?平面OPB,
∴PB⊥AD;
(Ⅱ)解:∵PA=PD=DA=2,
∴OP=OB=$\sqrt{3}$,
∵PB=$\sqrt{6}$,
∴OP2+OB2=PB2,
∴OP⊥OB,
∵OP⊥AD,AD∩OB=O,
∴OP⊥平面CBD,
△PBD中,PD=BD=2,PB=$\sqrt{6}$,∴S△PBD=$\frac{1}{2}•\sqrt{6}•\sqrt{4-(\frac{\sqrt{6}}{2})^{2}}$=$\frac{\sqrt{15}}{2}$
设点C到平面PBD的距离为h,则$\frac{1}{3}•\frac{\sqrt{15}}{2}h$=$\frac{1}{3}•\frac{\sqrt{3}}{4}•4•\sqrt{3}$=$\frac{2\sqrt{15}}{5}$.
点评 本题考查线面垂直的判定与性质,考查点到平面距离的计算,考查体积的计算,属于中档题.

练习册系列答案
相关题目
8.已知△ABC为等腰直角三角形,|CA|=|CB|,|AB|=4,O为AB中点,动点P满足条件:|PO|2=|PA|•|PB|,则线段CP长的最小值为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 4 |
15.从空间一点P向二面角α-l-β的两个面α、β分别作垂线PE、PF,E,F分别为垂足,若∠EPF=40°,则二面角的平面角的大小是( )
| A. | 40° | B. | 40°或140° | C. | 140° | D. | 50° |
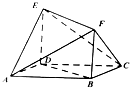 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=$\frac{π}{3}$.
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=$\frac{π}{3}$.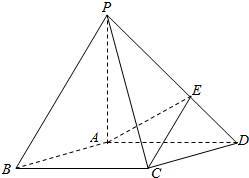 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E是PD的中点.
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E是PD的中点.