题目内容
如图多面体ABCDEF中,ABCD是边长为2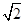 的正方形,AE⊥平面ABCD,BF∥AE且AE=2BF=4,则以下结论正确的是______________________.(写出所有正确结论的编号)
的正方形,AE⊥平面ABCD,BF∥AE且AE=2BF=4,则以下结论正确的是______________________.(写出所有正确结论的编号)
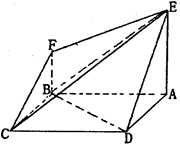
①CF∥DE;②BD∥平面CEF;③AF⊥平面BCE;
④平面CEF⊥平面ADE.
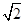 的正方形,AE⊥平面ABCD,BF∥AE且AE=2BF=4,则以下结论正确的是______________________.(写出所有正确结论的编号)
的正方形,AE⊥平面ABCD,BF∥AE且AE=2BF=4,则以下结论正确的是______________________.(写出所有正确结论的编号)
①CF∥DE;②BD∥平面CEF;③AF⊥平面BCE;
④平面CEF⊥平面ADE.
②③
试题分析:根据题意,由于面体ABCDEF中,ABCD是边长为2
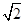 的正方形,AE⊥平面ABCD,BF∥AE且AE=2BF=4,那么可知①CF∥DE;要成立则D,C,E,F共面,不成立,②BD∥平面CEF;成立③AF⊥平面BCE;根据线面垂直的判定定理可知成立。对于④平面CEF⊥平面ADE,因为ABEF也垂直于平面ADE,显然不能垂直,故错误,因此答案为②③
的正方形,AE⊥平面ABCD,BF∥AE且AE=2BF=4,那么可知①CF∥DE;要成立则D,C,E,F共面,不成立,②BD∥平面CEF;成立③AF⊥平面BCE;根据线面垂直的判定定理可知成立。对于④平面CEF⊥平面ADE,因为ABEF也垂直于平面ADE,显然不能垂直,故错误,因此答案为②③点评:主要是考查了空间中的线面和面面的位置关系的运用,属于基础题 。

练习册系列答案
相关题目
 ,使得
,使得 ,命题q:
,命题q: 
 .则下列命题中真命题为( )
.则下列命题中真命题为( )



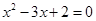 ,则
,则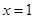 ”的逆否命题为:“若
”的逆否命题为:“若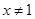 ,则
,则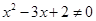 ”
”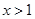 ”是“
”是“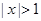 ”的充分不必要条件
”的充分不必要条件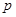 且
且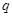 为假命题,则
为假命题,则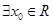 ,使得
,使得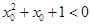 ”,则
”,则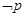 :“
:“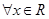 ,均有
,均有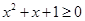 ”
”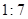 ;④平行圆锥轴的截面是一个等腰三角形.
;④平行圆锥轴的截面是一个等腰三角形.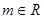 ,对
,对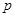 :
: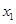 和
和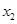 是方程
是方程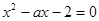 的两个根,不等式
的两个根,不等式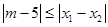 对任意实数
对任意实数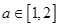 恒成立;
恒成立;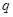 :函数
:函数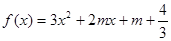 有两个零点,求使“
有两个零点,求使“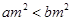 ,则
,则 ”的逆命题为真;
”的逆命题为真; 一定经过其样本数据点
一定经过其样本数据点 ,
, ,
, ,
, 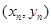 中的一个点;
中的一个点;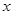 ,使得
,使得 ”的否定是“对任意实数
”的否定是“对任意实数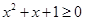 ”
”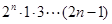 (
( )时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).
)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).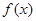 是
是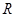 上的增函数,若
上的增函数,若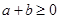 ,则
,则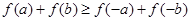 ”的逆否命题为真命题
”的逆否命题为真命题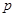 :“存在
:“存在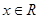 ,使得
,使得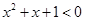 ”,则
”,则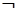
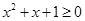 ”
”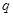 为假命题,则
为假命题,则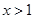 ”是“
”是“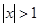 ”的充分不必要条件
”的充分不必要条件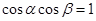 ,则
,则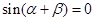 ;
; 与函数
与函数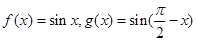 的图像分别交于点
的图像分别交于点 ,则
,则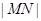 的最大值为
的最大值为 ;
; 为单调递增数列,则
为单调递增数列,则 取值范围是
取值范围是 ;
; 的通项
的通项 ,前
,前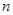 项和为
项和为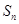 ,则使
,则使 的
的 使得
使得 ”的否定是( )
”的否定是( )