题目内容
已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=2AB=4．
（1）根据已经给出的此四棱锥的正视图，画出其俯视图和侧视图；
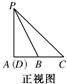
（2）证明：平面PAD⊥平面PCD．
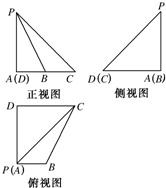解：（1）三视图如图所示（2）证明：∵PA⊥平面ABCD，PA?平面PAD，
∴平面PAD⊥平面ABCD．
又平面PAD∩平面ABCD=AD，
CD?平面ABCD，CD⊥AD，∴CD⊥平面PAD．
又CD?平面PCD，∴
分析：（1）利用三视图中正视图，俯视图和侧视图之间的对应关系“长对正，高平齐，宽相等“可画出其俯视图和侧视图．
（2）先证明平面PAD⊥平面ABCD，再证得CD⊥平面PAD即可得到平面PAD⊥平面PCD．
点评：本题考查平面和平面垂直的判定和性质和三视图中正视图，俯视图和侧视图之间的对应关系“长对正，高平齐，宽相等“．在证明面面垂直时，其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直
练习册系列答案
相关题目
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC，侧面PBC⊥底面ABCD，O是BC的中点．
已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，E为BC中点，AE与BD交于O点，AB=BC=2CD=2，BD⊥PE．
如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠DAB=∠ABC=90°，E是线段PC上一点，PC⊥平面BDE．