题目内容
已知点 是抛物线
是抛物线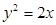 上的动点,
上的动点, 是抛物线的焦点,若点
是抛物线的焦点,若点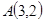 ,则
,则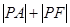 的最小值是 .
的最小值是 .
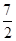
解析试题分析:过P作准线l的垂线PM,垂足为M,则|PF|=|PM|,所以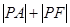 =|PA|+|PM|,
=|PA|+|PM|,
过A作AN垂直准线l,垂直为N,则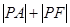 =|PA|+|PM|
=|PA|+|PM|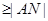 ,显然当点P为AN与抛物线的交点时,
,显然当点P为AN与抛物线的交点时,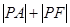 取得最小值|AN|=
取得最小值|AN|=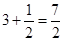 .
.
考点:抛物线的定义,标准方程及性质.
点评:解本小题的关键是把P到F的距离转化为P到准线的距离,从而转化为求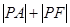 =|PA|+|PM|
=|PA|+|PM|
的最小值,再利用三角形两边之差小于第三边可知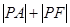 =|PA|+|PM|
=|PA|+|PM|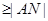 .到此问题得解.
.到此问题得解.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
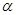 经过点
经过点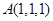 ,且
,且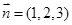 是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面
是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: ,则C表是长轴在x轴上的椭圆.
,则C表是长轴在x轴上的椭圆.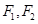 ,虚轴的一个端点
,虚轴的一个端点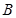 ,且
,且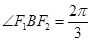 ,则此双曲线的离心率为 。
,则此双曲线的离心率为 。 时的椭圆的标准方程是 .
时的椭圆的标准方程是 .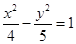 ,则离心率为 .
,则离心率为 .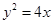 的准线方程是 .
的准线方程是 .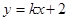 与双曲线
与双曲线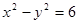 的右支相交于不同两点,则
的右支相交于不同两点,则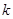 的取值范围是
的取值范围是 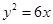 的准线方程为
的准线方程为