题目内容
20.已知a,b,c∈R,那么下列命题中正确的是( )| A. | 若a<b,则ac2<bc2 | B. | 若a>b>0,c<0,则$\frac{c}{a}<\frac{c}{b}$ | ||
| C. | 若a>b,则(a+c)2>(b+c)2 | D. | 若ab>0,则$\frac{a}{b}+\frac{b}{a}≥2$ |
分析 A.c=0时不成立;
B.由a>b>0,可得$\frac{1}{a}<\frac{1}{b}$,又c<0,利用不等式的基本性质即可得出;
C.若0>a+c>b+c,则(a+c)2>(b+c)2不成立;
D.利用基本不等式的性质即可判断出.
解答 解:A.c=0时不成立;
B.∵a>b>0,∴$\frac{1}{a}<\frac{1}{b}$,又c<0,则$\frac{c}{a}>\frac{c}{b}$,因此不正确;
C.若0>a+c>b+c,则(a+c)2>(b+c)2不成立;
D.∵ab>0,则$\frac{a}{b}+\frac{b}{a}≥2$$\sqrt{\frac{a}{b}•\frac{b}{a}}$=2,当且仅当a=b时取等号,因此正确.
故选:D.
点评 本题考查了不等式的性质与基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.在极坐标系中,曲线C:ρ=2sinθ上的两点A,B对应的极角分别为$\frac{2π}{3},\frac{π}{3}$,则弦长|AB|等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
11.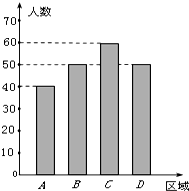 教育资源的不均衡是促进“择校热”的主要因素之一,“择校热”也是教育行政部门一直着力解决的问题.某社会调查机构为了调查学生家长对解决“择校热”的满意程度,从A,B,C,D四个不同区域内分别选择一部分学生家长作调查,每个区域选出的人数如条形图所示.为了了解学生家长的满意程度,对每位家长都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
教育资源的不均衡是促进“择校热”的主要因素之一,“择校热”也是教育行政部门一直着力解决的问题.某社会调查机构为了调查学生家长对解决“择校热”的满意程度,从A,B,C,D四个不同区域内分别选择一部分学生家长作调查,每个区域选出的人数如条形图所示.为了了解学生家长的满意程度,对每位家长都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
(Ⅰ)若家长甲来自A区域,求家长甲的调查问卷被选中的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的家长中再选出2人进行面谈,求这2人中至少有一人来自D区域的概率.
 教育资源的不均衡是促进“择校热”的主要因素之一,“择校热”也是教育行政部门一直着力解决的问题.某社会调查机构为了调查学生家长对解决“择校热”的满意程度,从A,B,C,D四个不同区域内分别选择一部分学生家长作调查,每个区域选出的人数如条形图所示.为了了解学生家长的满意程度,对每位家长都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
教育资源的不均衡是促进“择校热”的主要因素之一,“择校热”也是教育行政部门一直着力解决的问题.某社会调查机构为了调查学生家长对解决“择校热”的满意程度,从A,B,C,D四个不同区域内分别选择一部分学生家长作调查,每个区域选出的人数如条形图所示.为了了解学生家长的满意程度,对每位家长都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:| 满意 | 一般 | 不满意 | |
| A区域 | 50% | 25% | 25% |
| B区域 | 80% | 0 | 20% |
| C区域 | 50% | 50% | 0 |
| D区域 | 40% | 20% | 40% |
(Ⅱ)若想从调查问卷被选中且填写不满意的家长中再选出2人进行面谈,求这2人中至少有一人来自D区域的概率.
8.将函数y=cosx的图象向右平移$\frac{π}{6}$个单位长度,再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
| A. | $y=cos(\frac{1}{2}x-\frac{π}{6})$ | B. | $y=cos(\frac{1}{2}x-\frac{π}{3})$ | C. | $y=cos(2x-\frac{π}{6})$ | D. | $y=cos(2x-\frac{π}{3})$ |
12.在单调递增的等差数列{an}中,若a3=1,a2a4=$\frac{3}{4}$,则a1=( )
| A. | -1 | B. | 0 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
9.曲线y=$\frac{1-2x}{{x}^{2}}$在点(-1,3)处的切线方程为( )
| A. | y=4x-7 | B. | y=4x+7 | C. | y=-4x-1 | D. | y=-4x+3 |
18.已知f(x)是定义在R上的奇函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=ex-1,则f(-2014)+f(2015)=( )
| A. | 1-e | B. | e-1 | C. | -1-e | D. | e+1 |