题目内容
2.已知函数$f(x)=\frac{x+a}{e^x}$.(Ⅰ)若f(x)在区间(-∞,2)上为单调递增函数,求实数a的取值范围;
(Ⅱ)若a=0,x0<1,设直线y=g(x)为函数f(x)的图象在x=x0处的切线,求证:f(x)≤g(x).
分析 (Ⅰ)求出函数的导函数$f′(x)=-\frac{x-(1-a)}{{e}^{x}}$,通过f′(x)≥0对x∈(-∞,2)恒成立,推出1-a≥2,即可求出a的范围.
(Ⅱ)利用a=0,化简f(x)=$\frac{x}{{e}^{x}}$.通过函数f(x)在x=x0处的切线方程为y=g(x)=f'(x0)(x-x0)+f(x0)
讨论当x=x0时,f(x)=g(x);当x≠x0时,利用分析法证明f(x)<g(x);构造函数h(x)=f(x)-g(x)=f(x)-f'(x0)(x-x0)-f(x0),求出h'(x)=$\frac{(1-x){e}^{{x}_{0}}-(1-{x}_{0}){e}^{x}}{{e}^{x+{x}_{0}}}$,构造新函数$ϕ(x)=(1-x){e^{x_0}}-(1-{x_0}){e^x}$,x∈R,利用公式的导数求解函数的最值,然后推出结论.
解答 (本题满分13分)
解:(Ⅰ)由已知函数$f(x)=\frac{x+a}{e^x}$,$f′(x)=-\frac{x-(1-a)}{{e}^{x}}$,
由已知f′(x)≥0对x∈(-∞,2)恒成立,
故,x≤1-a对x∈(-∞,2)恒成立,得1-a≥2,
∴a≤-1为所求.…(4分)
(Ⅱ)证明:a=0,则f(x)=$\frac{x}{{a}^{x}}$.
函数f(x)在x=x0处的切线方程为y=g(x)=f'(x0)(x-x0)+f(x0)
当x=x0时,f(x)=g(x);
当x≠x0时,要证f(x)<g(x);
即证 f(x)-g(x)<0 …(6分)
令h(x)=f(x)-g(x)=f(x)-f'(x0)(x-x0)-f(x0)h'(x)=f'(x)-f'(x0)=$\frac{1-x}{e^x}-\frac{{1-{x_0}}}{{{e^{x_0}}}}=\frac{{(1-x){e^{x_0}}-(1-{x_0}){e^x}}}{{{e^{x+{x_0}}}}}$
设$ϕ(x)=(1-x){e^{x_0}}-(1-{x_0}){e^x}$,x∈R
则$ϕ'(x)=-{e^{x_0}}-(1-{x_0}){e^x}$,∵x0<1,∴ϕ'(x)<0
∴ϕ(x)在R上单调递减,而ϕ(x0)=0…(10分)
∴当x<x0时,ϕ(x)>0,当x>x0时,ϕ(x)<0
即当x<x0时,h'(x)>0,当x>x0时h'(x)<0
∴h(x)在区间(-∞,x0)上为增函数,在区间(x0,+∞)上为减函数
∴x≠x0时,h(x)<h(x0)=0,即有f(x)<g(x)
综上,f(x)≤g(x)…(13分)
点评 本题考查函数的导数的应用,构造法以及新函数的导数的综合应用,函数恒成立问题的转化方法,考查分析问题解决问题的能力.

| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 8 | D. | 6 |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | 16 | B. | 2 | C. | 6 4 | D. | 128 |
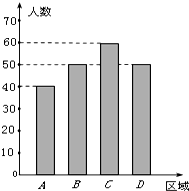 教育资源的不均衡是促进“择校热”的主要因素之一,“择校热”也是教育行政部门一直着力解决的问题.某社会调查机构为了调查学生家长对解决“择校热”的满意程度,从A,B,C,D四个不同区域内分别选择一部分学生家长作调查,每个区域选出的人数如条形图所示.为了了解学生家长的满意程度,对每位家长都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
教育资源的不均衡是促进“择校热”的主要因素之一,“择校热”也是教育行政部门一直着力解决的问题.某社会调查机构为了调查学生家长对解决“择校热”的满意程度,从A,B,C,D四个不同区域内分别选择一部分学生家长作调查,每个区域选出的人数如条形图所示.为了了解学生家长的满意程度,对每位家长都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:| 满意 | 一般 | 不满意 | |
| A区域 | 50% | 25% | 25% |
| B区域 | 80% | 0 | 20% |
| C区域 | 50% | 50% | 0 |
| D区域 | 40% | 20% | 40% |
(Ⅱ)若想从调查问卷被选中且填写不满意的家长中再选出2人进行面谈,求这2人中至少有一人来自D区域的概率.
| A. | -1 | B. | 0 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |