题目内容
19．实数x，y满足$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y≤1}\end{array}\right.$，则z=x-y的最大值是3．分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案．
解答 解：由约束条件$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y≤1}\end{array}\right.$作出可行域如图，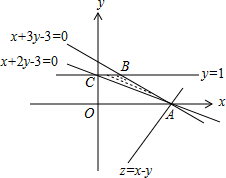
化目标函数z=x-y为直线方程斜截式y=x-z，
由图可知，当直线y=x-z过A（3，0）时，直线在y轴上的截距最小，z最大，最大值为3-0=3．
故答案为：3．
点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
9．已知a1=a2015=1，且|an+1|=|an+1|（n∈N*），则a1+a2+…+a2015=（ ）
| A． | 2015 | B． | 2016 | C． | -1006 | D． | -1007 |
10．在极坐标系中，曲线C：ρ=2sinθ上的两点A，B对应的极角分别为$\frac{2π}{3}，\frac{π}{3}$，则弦长|AB|等于（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
7．已知等差数列{an}的前9项的和为27，则${2^{{a_2}+{a_8}}}$=（ ）
| A． | 16 | B． | 2 | C． | 6 4 | D． | 128 |
4．在△ABC中，角A，B，C所对的边分别为a，b，c，且a=1，B=45°，S△ABC=2，则 b等于（ ）
| A． | $4\sqrt{2}$ | B． | 5 | C． | 41 | D． | $5\sqrt{2}$ |
11．
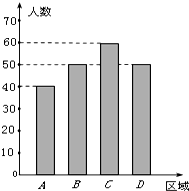教育资源的不均衡是促进“择校热”的主要因素之一，“择校热”也是教育行政部门一直着力解决的问题．某社会调查机构为了调查学生家长对解决“择校热”的满意程度，从A，B，C，D四个不同区域内分别选择一部分学生家长作调查，每个区域选出的人数如条形图所示．为了了解学生家长的满意程度，对每位家长都进行了问卷调查，然后用分层抽样的方法从调查问卷中抽取20份进行统计，统计结果如下面表格所示：
（Ⅰ）若家长甲来自A区域，求家长甲的调查问卷被选中的概率；
（Ⅱ）若想从调查问卷被选中且填写不满意的家长中再选出2人进行面谈，求这2人中至少有一人来自D区域的概率．
教育资源的不均衡是促进“择校热”的主要因素之一，“择校热”也是教育行政部门一直着力解决的问题．某社会调查机构为了调查学生家长对解决“择校热”的满意程度，从A，B，C，D四个不同区域内分别选择一部分学生家长作调查，每个区域选出的人数如条形图所示．为了了解学生家长的满意程度，对每位家长都进行了问卷调查，然后用分层抽样的方法从调查问卷中抽取20份进行统计，统计结果如下面表格所示：| 满意 | 一般 | 不满意 | |
| A区域 | 50% | 25% | 25% |
| B区域 | 80% | 0 | 20% |
| C区域 | 50% | 50% | 0 |
| D区域 | 40% | 20% | 40% |
（Ⅱ）若想从调查问卷被选中且填写不满意的家长中再选出2人进行面谈，求这2人中至少有一人来自D区域的概率．
8．将函数y=cosx的图象向右平移$\frac{π}{6}$个单位长度，再把所得图象上各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是（ ）
| A． | $y=cos（\frac{1}{2}x-\frac{π}{6}）$ | B． | $y=cos（\frac{1}{2}x-\frac{π}{3}）$ | C． | $y=cos（2x-\frac{π}{6}）$ | D． | $y=cos（2x-\frac{π}{3}）$ |
9．曲线y=$\frac{1-2x}{{x}^{2}}$在点（-1，3）处的切线方程为（ ）
| A． | y=4x-7 | B． | y=4x+7 | C． | y=-4x-1 | D． | y=-4x+3 |