题目内容
已知实系数方程x2+(m+1)x+m+n+1=0的两个实数根分别是x1,x2,且0<x1<1,x2>1,则u=
的取值范围是( )
| m2+n2 |
| mn |
分析:首先根据所给的一元二次方程的根的范围,表示出m,n之间的关系,得到不等式组,画出可行域,求出
的范围,做出它的倒数的范围,根据基本不等式表示出最大值,得到结果.
| n |
| m |
解答:解:令f(x)=x2+(m+1)x+m+n+1,
由题意0<x1<1,x2>1,知,
即
不等式组表示区域如图阴影部分.
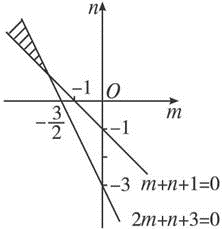
表示点P(m,n)与原点连线的斜率.
∴-2<
<-
,
-2<
<-
,
∵
与
的符号是负数,得到根据基本不等式知
+
≤-2
∵
与
取得最值的时候正好相反,即一个取得最大值时,另一个取得最小值,
∵u=
=
+
∈(-
,-2]
故选A.
由题意0<x1<1,x2>1,知,
|
|
不等式组表示区域如图阴影部分.

| n |
| m |
∴-2<
| n |
| m |
| 1 |
| 2 |
-2<
| m |
| n |
| 1 |
| 2 |
∵
| m |
| n |
| n |
| m |
| m |
| n |
| n |
| m |
∵
| m |
| n |
| n |
| m |
∵u=
| m2+n2 |
| mn |
| n |
| m |
| m |
| n |
| 5 |
| 2 |
故选A.
点评:本题考查线性规划的应用,考查基本不等式求最值,考查一元二次方程的根与系数的关系,本题解题的关键是对所给的代数式变形整理,再根据线性规划得到要用的范围,本题是一个中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实系数方程x2+ax+2b=0的一个根大于0且小于1,另一根大于1且小于2,则
的取值范围是( )
| b-2 |
| a-1 |
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(0,
|
已知实系数方程x2+ax+1=0的一个实根在区间(1,2)内,则a的取值范围为( )
| A、(-2,-1) | ||
B、(-
| ||
| C、(1,2) | ||
D、(2,
|
已知实系数方程x2+(a+1)x+a+b+1=0的两根分别为一个椭圆和一个双曲线的离心率,则
的取值范围是( )
| b |
| a |
| A、(-2,-1) | ||
B、(-1,-
| ||
C、(-2,-
| ||
| D、(-2,+∞) |