题目内容
已知实系数方程x2+ax+2b=0的一个根大于0且小于1，另一根大于1且小于2，则
的取值范围是（ ）
| b-2 |
| a-1 |
A、（
| ||||
B、（
| ||||
C、（-
| ||||
D、（0，
|
分析：先根据根的分布列出约束条件画出可行域，再利用几何意义求最值，本例中，
的取值的几何意义是斜率．
| b-2 |
| a-1 |
解答：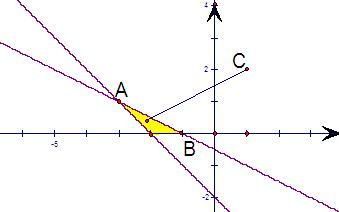
解：设f（x）=x2+ax+2b，由题意得：
，即
，
在坐标系aOb中画出上述不等式组表示的平面区域，
由题意，约束条件表示的平面区域为阴影部分（不包括边界）．
目标函数
的几何意义为可行域内的连接两点（x，y）与点C（1，2）的直线的斜率，
根据平面区域，易求得
的最大值为kBC=1，最小值为kAC=
，
故得
∈（
，1），
故选A
解：设f（x）=x2+ax+2b，由题意得：
|
|
在坐标系aOb中画出上述不等式组表示的平面区域，
由题意，约束条件表示的平面区域为阴影部分（不包括边界）．
目标函数
| b-2 |
| a-1 |
根据平面区域，易求得
| b-2 |
| a-1 |
| 1 |
| 4 |
故得
| b-2 |
| a-1 |
| 1 |
| 4 |
故选A
点评：本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题．解决时，首先要解决的问题是让学生明白题目中目标函数的意义．
练习册系列答案
相关题目
已知实系数方程x2+ax+1=0的一个实根在区间（1，2）内，则a的取值范围为（ ）
| A、（-2，-1） | ||
B、(-
| ||
| C、（1，2） | ||
D、(2，
|
已知实系数方程x2+（a+1）x+a+b+1=0的两根分别为一个椭圆和一个双曲线的离心率，则
的取值范围是（ ）
| b |
| a |
| A、（-2，-1） | ||
B、(-1，-
| ||
C、(-2，-
| ||
| D、（-2，+∞） |