题目内容
(2013•南京二模)在平面直角坐标系xOy中,已知双曲线C:
-
=1.设过点M(0,1)的直线l与双曲线C交于A、B两点,若
=2
,则直线l的斜率为
| x2 |
| 4 |
| y2 |
| 3 |
| AM |
| MB |
±
| 1 |
| 2 |
±
.| 1 |
| 2 |
分析:设直线AB方程为y=kx+1,与双曲线方程联解得(3-4k2)x2-8kx-16=0.设A(x1,y1),B(x2,y2),由根与系数的关系可得x1+x2=
且x1x2=
,根据
=2
得x1=-2x2,将三个式子联解,即可得到直线l的斜率.
| 8k |
| 3-4k2 |
| -16 |
| 3-4k2 |
| AM |
| MB |
解答: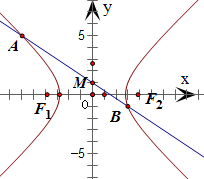 解:设直线AB方程为y=kx+1,与双曲线
解:设直线AB方程为y=kx+1,与双曲线
-
=1消去y,
得(3-4k2)x2-8kx-16=0.
设A(x1,y1),B(x2,y2),
由根与系数的关系,得
…(1)
∵
=2
,可得x1=-2x2,∴代入(1)得
,
消去x2得-2(
)2=
,解之得k2=
,得k=±
故答案为:±
 解:设直线AB方程为y=kx+1,与双曲线
解:设直线AB方程为y=kx+1,与双曲线| x2 |
| 4 |
| y2 |
| 3 |
得(3-4k2)x2-8kx-16=0.
设A(x1,y1),B(x2,y2),
由根与系数的关系,得
|
∵
| AM |
| MB |
|
消去x2得-2(
| 8k |
| 3-4k2 |
| -16 |
| 3-4k2 |
| 1 |
| 4 |
| 1 |
| 2 |
故答案为:±
| 1 |
| 2 |
点评:本题给出经过点M(0,1)的直线l交双曲线于AB两点,在已知
=2
的情况下求直线的斜率.着重考查了双曲线的标准方程、简单几何性质和直线与双曲线位置关系等知识,属于中档题.
| AM |
| MB |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
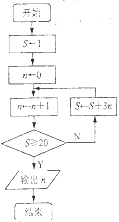 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是